Abelian group
Abelian groups generalize the arithmetic concept of addition of integers. (They were named after Niels Henrik Abel.[1]).
- Thus, in abstract algebra, an abelian group, is a commutative group, previously called a `symplectic' group.
An abelian group is defined as a set, 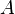 , together with an operation "
, together with an operation "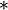 " which is commutative, that is, for any elements
" which is commutative, that is, for any elements  and
and 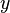 of
of 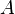 one has that:
one has that:
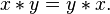
The operation of addition of integers obviously has the property of commutativity.
Notes
- 1. The collection of all Abelian groups, together with the group homomorphisms between them, forms the category
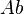 , the prototype of an Abelian category.
, the prototype of an Abelian category.
- 2. Almost all of the well-known algebraic structures other than Boolean algebras, are undecidable (see Gödel's theorems; see also the following note). It was therefore rather surprising when one of Tarski's student, Szmielew proved in 1955 that the first order theory of abelian groups-- unlike its nonabelian counterpart-- is decidable. This important result provides an interesting link between the category of Abelian groups and that of Boolean algebras.
- 3. Moreover, one expect that the theory of centered Łukasiewicz logic algebras should also be decidable because there is a fundamental, categorical adjointness defined between the category of centered Łukasiewicz logic algebras and that of Boolean logic algebras[2]. Note also that general Łukasiewicz n-valued logic algebras are `'noncommutative [3]
References
- ↑ Jacobson (2009), p. 41
- ↑ http://aux.planetphysics.us/files/papers/100/NvalLogicsGG.pdf Georgescu, G. 2006, N-valued Logics and Łukasiewicz-Moisil Algebras, Axiomathes, 16 (1-2): 123-136.
- ↑ http://images.planetphysics.us/files/lec/294/CategoryOfLMnLogicAlgebrasPP.pdf Topic: Algebraic category of Łukasiewicz-Moisil n-valued logic algebras.
- Jacobson, Nathan (2009). Basic Algebra I (2nd ed.). Dover Publications. ISBN 978-0-486-47189-1.
- Szmielew, Wanda (1955). "Elementary properties of abelian groups". Fundamenta Mathematicae 41: 203–271.
- Cox, David (2004). Galois Theory. Wiley-Interscience.
- Fuchs, László (1970). Infinite Abelian Groups, Vol. I. Pure and Applied Mathematics. 36-I. Academic Press.
This article is issued from Wikiversity - version of the Sunday, June 10, 2012. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.