Abelian category

An Abelian category is defined as follows according to Barry Mitchell (1965).

Definition: "An Abelian category is an exact, additive category with finite products."

The following theorem from ref.[2] is also relevant as it specifies the key properties of all Abelian categories^[1] :

“The following statements are equivalent:

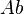$Ab$ is an Abelian category;
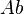$Ab$ has kernels, cokernels, finite products, finite coproducts, and is both normal and comormal;
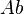$Ab$ has pushouts and pullbacks and is both normal and conormal”.

References

1. ↑ http://planetphysics.us/encyclopedia/AbelianCategory2.html The Fundamental Abelian Category Theorem
2. Barry Mitchell. "Theory of Categories". Academic Press: New York and London, 1965, (Theorem 20.1 on p.33).

This article is issued from Wikiversity - version of the Tuesday, June 12, 2012. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.