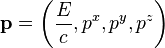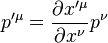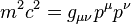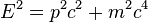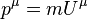4-momentum

Including a time element of energy as

$\mathbf{p}=\left(\frac{E}{c},p^x ,p^y ,p^z \right)$

This four element vector transforms as a tensor

$p'^\mu =\frac{\partial x'^\mu }{\partial x^\nu }p^{\nu }$

And as such constitutes a four-vector, a rank 1 tensor, called the 4-momentum. The mass of a particle is an invariant given by the spacetime length of the 4-momentum according to

$m^2c^2 = g_{\mu \nu }p^\mu p^\nu$

which for the metric of special relativity yeilds

$E^2 = p^2 c^2 + m^2 c^4$

For a particle with mass, the 4-momentum can be related to the 4-velocity by

$p^\mu = mU^\mu$

This article is issued from Wikiversity - version of the Monday, December 16, 2013. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.