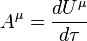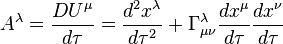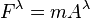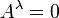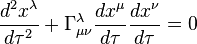4-acceleration

4-acceleration is a four-vector which in special relativity is the proper time derivative of 4-velocity.

$A^\mu = \frac{dU^\mu }{d\tau }$

When curvalinear coordinates are used such as in general relativity, the acceleration 4-vector is the covariant derivative of 4-velocity with respect to proper time (see operator of proper-time-derivative)

$A^\lambda = \frac{DU^\mu }{d\tau } = \frac{d^2 x^\lambda }{d\tau^2}+\Gamma ^\lambda _{\mu \nu }\frac{dx^\mu }{d\tau }\frac{dx^\nu }{d\tau }$

It relates to the force Four-force by Newton's second law

$F^\lambda = mA^\lambda$

where the mass 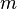$m$ is an invariant.

And in the Absence of a 4-force this

$A^\lambda = 0$

gives the geodesic equation

$\frac{d^2 x^\lambda }{d\tau^2}+\Gamma ^\lambda _{\mu \nu }\frac{dx^\mu }{d\tau }\frac{dx^\nu }{d\tau }=0$

This article is issued from Wikiversity - version of the Monday, August 18, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.