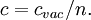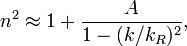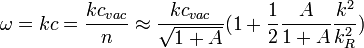Waves/Light

< Waves

Waves : 1 Dimensional Waves
1 - 2 - 3 - 4 - 5 - 6 - 7 - 8 - 9 - 10 - 11 - 12 - 13
Examples - Problems - Solutions - Terminology

Light

Light moves in a vacuum at a speed of 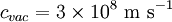$c_{vac} = 3 \times 10^8 \mbox{ m} \mbox{ s}^{-1}$ . In transparent materials it moves at a speed less than 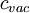$c_{vac}$ by a factor 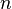$n$ which is called the refractive index of the material:

c = c_{vac} / n .

Often the refractive index takes the form

n^2 \approx 1 + \frac{A}{1 - (k/k_R )^2} ,

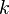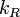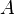where $k$ is the wavenumber and $k_R$ and $A$ are constants characteristic of the material. The angular frequency of light in a transparent medium is thus

\omega = kc = \frac{k c_{vac}}{n} \approx \frac{k c_{vac}}{\sqrt{1+A}}(1+ \frac{1}{2}\frac{A}{1+A}\frac{k^2}{k^2_R})

so the frequency increases slightly with increasing k. Typically, when k is near k_R, the material becomes opaque.

Ultimately, this is due to resonance between the light and the atoms of the materials.

Waves : 1 Dimensional Waves
1 - 2 - 3 - 4 - 5 - 6 - 7 - 8 - 9 - 10 - 11 - 12 - 13
Examples - Problems - Solutions - Terminology

This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.