Trigonometry/The most Difficult Triangles to Solve

Given SSA (Two Sides and an Angle Not Included by the Two Sides - the Ambiguous Case)

In the diagram below, the red arcs indicate some points at the same distance from the bottom left corner of the triangle. These are points that make one of the side lengths right. The missing corner of the triangle must be on one of the points where the red arcs intersect the sloping dotted line.

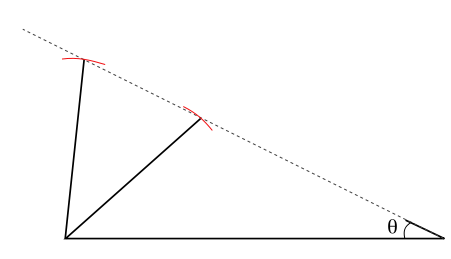
Look at the diagram above. We run into trouble. There are two possible solutions. The given information may not uniquely determine a triangle. It's worse than that. There may not be a solution at all, if angle $\theta$ is too large.

Here's how we proceed.

One of the two given sides, side $a$ is opposite the given angle, so we can apply the Law of Sines to try to find the angle opposite the other given side. When we do this (given sides $a$ and $b$ and angle $A$ ), we'll have $\sin(B)={\frac {b\sin(\theta )}{a}}$ and there are three possibilities:

Either $\sin(B)>1$ , $\sin(B)=1$ , or $\sin(B)<1$ .

If $\sin(B)>1$ , then there is no angle $B$ that meets the given information, so no triangle can be formed with the given sides and angle. This is because the side is too short to reach the dotted line, whatever position it is in.
If $\sin(B)=1$ , then we have a right triangle with right angle at $B$ and we can proceed as above for right triangles.
If $\sin(B)<1$ and the side opposite the given angle is shorter than the other given side, then there are two possible measures for angle $B$ , one acute (the inverse sine of the value of $\sin(B)$ ) and one obtuse (the supplement of the acute one, i.e. 180º less that angle). Whichever of the two angles we choose, we can find the missing information as above now that we have two angles. Thus there are two possible solutions.
If $\sin(B)<1$ and the side opposite the given angle is longer than the other given side, then again there may appear to be two solutions, but one is invalid since we will find that two angles add to more than 180º so the third angle would be negastive. Thus there is only one possible solution. (If the two given sides are of equal length, the second solution would be a triangle of zero area where these two sides coincide and the third side is of zero length.)

The case $\sin(B)=1$

Thanks to the Pythagorean Theorem, it is possible to prove that two right triangles are congruent if they have equal hypotenuses and also one other pair of sides is equal. (However, Euclid proves this theorem without needing Pythagoras' Theorem.)

Proof

Okay, we already know the theorem:

a^{2}+b^{2}=c^{2}

Right?

As a result, you see that it can be turned around to yield the formula $c^{2}-b^{2}=a^{2}$ . This means that, if you know the hypotenuse and one leg of a triangle, you can calculate the length of the second leg. This is not only important in and of itself, but also because it means that you know the lengths of all three sides of the triangle, and there is only one unique triangle with three particular side lengths, which means that if you know that the hypotenuse and one leg of two triangles are congruent, you also know that the two triangles are congruent!

This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.