Trigonometry/Sum into Product

< Trigonometry

These are exercises on the formulae derived in Book 1 for converting the sum or difference of two sines or two cosines into a product.

[1] 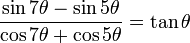$\frac{ \sin 7 \theta - \sin 5 \theta }{ \cos 7 \theta + \cos 5 \theta }=\tan \theta$

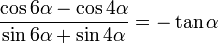
[2] $\frac{ \cos 6 \alpha - \cos 4 \alpha }{ \sin 6 \alpha + \sin 4 \alpha }=- \tan \alpha$

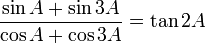
[3] $\frac{ \sin A + \sin 3A}{ \cos A + \cos 3A}=\tan 2A$

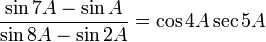
[4] $\frac{ \sin 7A - \sin A }{\sin 8A - \sin 2A}=\cos 4A \sec5A$

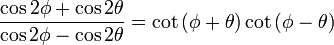
[5] $\frac{\cos 2\phi + \cos 2\theta}{\cos 2\phi - \cos 2\theta}=\cot \left(\phi + \theta \right)\cot \left( \phi - \theta \right)$

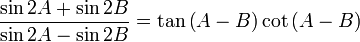
[6] $\frac{\sin 2A + \sin 2B}{\sin 2A - \sin 2B}=\tan \left(A - B\right) \cot \left( A - B \right)$

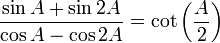
[7] $\frac{\sin A + \sin 2A}{\cos A - \cos 2A}=\cot \left( \frac{A}{2} \right)$

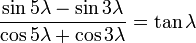
[8] $\frac{\sin 5\lambda - \sin 3\lambda}{\cos 5\lambda + \cos 3\lambda}=\tan \lambda$

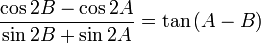
[9] $\frac{\cos 2B - \cos 2A}{\sin 2B + \sin 2A}=\tan \left(A - B \right)$

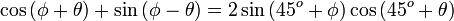
[10] $\cos \left( \phi + \theta \right) + \sin \left( \phi - \theta \right)=2\sin \left(45^o + \phi \right) \cos \left( 45^o + \theta \right)$

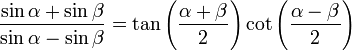
[11] $\frac{\sin \alpha + \sin \beta}{\sin \alpha - \sin \beta}=\tan \left( \frac{\alpha + \beta}{2} \right)\cot \left( \frac{\alpha - \beta}{2} \right)$

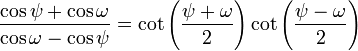
[12] $\frac{\cos \psi + \cos \omega}{\cos \omega - \cos \psi}=\cot \left( \frac{\psi + \omega}{2} \right) \cot \left( \frac{\psi - \omega}{2} \right)$

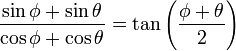
[13] $\frac{\sin \phi + \sin \theta}{\cos \phi + \cos \theta}=\tan \left( \frac{\phi + \theta}{2} \right)$

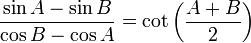
[14] $\frac{\sin A - \sin B}{\cos B - \cos A}=\cot \left( \frac{A + B}{2} \right)$

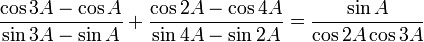
[15] $\frac{\cos 3A - \cos A}{\sin 3A - \sin A} + \frac{\cos 2A - \cos 4A}{\sin 4A - \sin 2A}=\frac{\sin A}{\cos 2A \cos 3A}$

[16] $a \cos \phi + b \sin \phi = \sqrt{a^2 + b^2}\cos[\phi-\tan^{-1}(\frac{b}{a})]$

This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.