Trigonometry/Solving Triangles Given ASA

< Trigonometry

One of the most common applications of trigonometry is solving triangles—finding missing sides and/or angles given some information about a triangle. The area of the triangle may also be required.

We can reconstruct the triangle given:

ASA Angle-Side-Angle (see illustration below).
AAS Angle-Angle-Side (see later on this page).
SAS Side-Angle-Side (see next page).
SSA Side-Side-Angle (later in this book). In the SSA case we may have one, two or no possible solutions.

Given ASA (Side and angles at each end of that side)

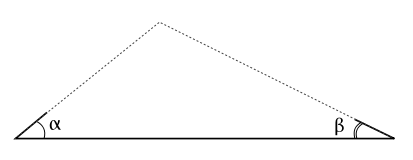
Given two angles, we can find the third angle (since the sum of the measures of the three angles in a triangle is $180^{\circ }$ .

The missing angle, $\theta$ is given by:

\theta =180^{\circ }-(\alpha +\beta )

Knowing all three angles and one side, we can use the Law of Sines to find the missing sides.

In the illustration if the side we are given is the base and has length $c$ , then the side opposite the angle $\alpha$ has length $a$ given by:

a=c\cdot {\frac {\sin(\alpha )}{\sin(\theta )}}

Check This

Check that this follows from the law of sines.

Now is also a good time to check that you can derive the law of sines for yourself. If given a problem triangle like this one in an exam, you might be asked both to find its missing sides and to derive the law of sines.

The area may then be found from Heron's Formula, or more easily by the formulae given in Law of Sines.

Given AAS (one side and two other angles)

Again we can work out the missing angle, since they sum to $180^{\circ }$ . From there on we have the same information as after the first step in the ASA case.

Exercises

Exercise 1: Easy angles I

A triangle $\Delta ABC$ has:

Side

\overline {BC}

of 30m

\angle ABC=30^{\circ }

and

\angle BCA=45^{\circ }

Draw a rough diagram.

What are the lengths of the remaining sides, and what is the missing angle?

Exercise 2: Easy angles II

A triangle $\displaystyle \Delta ABC$ has:

Side

\overline {BC}

of 30m

\angle BCA=30^{\circ }

and

\angle CAB=45^{\circ }

Draw a rough diagram.

What are the lengths of the remaining sides, and what is the missing angle?

Exercise 3: Similar/Congruent?

Are these two triangles in Exercise 1 and Exercise 2:

Similar to each other?
Congruent to each other?

This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.