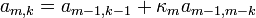Signal Processing/Lattice Predictors
< Signal ProcessingLevinson-Durbin Algorithm
The Levinson-Durbin Algorithm is a direct method to solve the augmented Wiener-Hopf equations for the lattice predictor-error coefficients and the predictor-error power. The Levinson-Durbin algorithm uses the filter coefficients of an order m filter to compute the coefficients of an order m + 1 order filter.
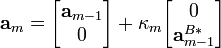
There are two parts to the Levinson-Durbin Algorithm. The first part is a method to compute the tap-weight vector am using the tap-weight vector of a lower-order filter, am-1:
In scalar form, this equation becomes:
This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.