Puzzles/Statistical puzzles/Summing n/Solution
< Puzzles < Statistical puzzles < Summing nThe solution is easily found if the problem is restated graphically. Consider n=3, k=2. Possible sums are 3 = 0+3, 3 = 1 + 2. A graphical representation could be:
||ooo |o|oo
, respectively, with the bars representing seperations between the summands and 'o's representing the value of the summands. Then obviously the problems is equivalent to finding the number of ways to distribute  bars among
bars among 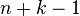 slots, since we need only
slots, since we need only  bars to partition the space into
bars to partition the space into 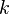 summands. Therefore the solution is
summands. Therefore the solution is
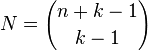 ,
if
,
if 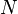 denotes the number of unique sums.
denotes the number of unique sums.
For the next part, set aside 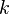 'o's since each partition has to have atleast
'o's since each partition has to have atleast  'o'. Now the problem reduces to the previous one with a reduced value of
'o'. Now the problem reduces to the previous one with a reduced value of 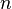 i.e.
i.e.  . So the solution is
. So the solution is
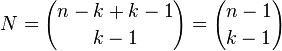 ,
,
if 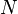 denotes the number of unique sums.
denotes the number of unique sums.
This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.