Puzzles/Statistical puzzles/Summing n

Puzzles | Statistical puzzles | Summing n

Given a target sum 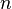$n$ , you can choose 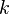$k$ summands each of which is a number, 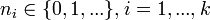$n_i \in \{0, 1, ...\}, i = 1, ..., k$ , such that 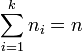$\sum_{i=1}^{k}{n_i} = n$ . How many ways are there of doing this?

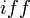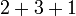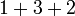Here the notion of a sum is same as that of a permutation, so two sums are same $iff$ they contain the same summands in the same order. E.g. $2+3+1$ and $1+3+2$ are not the same.

While you are at it, whats the answer, if 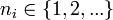$n_i \in \{1, 2, ...\}$ ?

solution

This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.