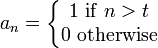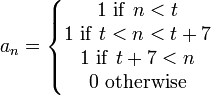Puzzles/Easy Sequence 10/Solution

< Puzzles < Easy Sequence 10

If one indexes the sequence from t, then the function for each term is trivially

a_n = \left\{\begin{matrix} 1\ \mathrm{if}\ n > t \\ 0\ \mathrm{otherwise} \end{matrix}\right.

Because this is the end of the easy sequences, you get something a bit more tricky - another solution:

a_n = \left\{\begin{matrix} 1\ \mathrm{if}\ n < t \\ 1\ \mathrm{if}\ t < n < t + 7 \\ 1\ \mathrm{if}\ t + 7 < n \\ 0\ \mathrm{otherwise} \end{matrix}\right.

Part of what mathematicians do is look for patterns. But be warned, just because it *looks* like it's doing something doesn't mean it's going to keep doing it forever! Showing that something does actually follow a pattern is some of what mathematicians spend their time on. But don't worry about that now, go look at some more sequences!

A bit too trivial for my liking, what about

$a_n = (n + 4)\ \mathbf{div}\ 6$

resulting in 0, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2...

What about any of these?

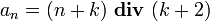$a_n = (n + k)\ \mathbf{div}\ (k+2)$ with k >= 4

The sequence wasn´t supposed to necessarily change from 1 to 2 exactly after the ellipsis ("...").

another solution: 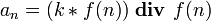$a_n = (k*f(n))\ \mathbf{div}\ f(n)$ with $k \in \ ]1,2[$

f(n) = f(n-1) ! for n > 1 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1...

This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.