Physics Study Guide/Logs

Review of logs

Been a while since you used logs? Here is a quick refresher for you.

The log (short for logarithm) of a number N is the exponent used to raise a certain "base" number B to get N. In short, 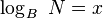$\log_B\ N = x$ means that $B^x = N$ .

Typically, logs use base 10. An increase of "1" in a base 10 log is equivalent to an increase by a power of 10 in normal notation. In logs, "3" is 100 times the size of "1". If the log is written without an explicit base, 10 is (usually) implied.

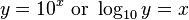y=10^x\ \mathrm{or}\ \log_{10}y=x\

therefore: log(10^–12) = –12

also: log(1000) = 3

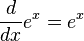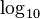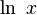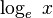Another common base for logs is the trancendental number $e$ , which is approximately 2.7182818.... Since $\frac{d}{dx} e^x = e^x$ , these can be more convenient than $\log_{10}$ . Often, the notation $\ln\ x$ is used instead of $\log_e\ x$ .

The following properties of logs are true regardless of whether the base is 10, $e$ , or some other number.

logA + logB = log(AB)

logA – logB = log(A/B)

log(A^B) = B log(A)

Adding the log of A to the log of B will give the same result as taking the log of the product A times B.

Subtracting the log of B from the log of A will give the same result as taking the log of the quotient A divided by B.

The log of (A to the Bth power) is equal to the product (B times the log of A).

A few examples:
log(2) + log(3) = log(6)
log(30) – log(2) = log(15)
log(8) = log(2³) = 3log(2)

This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.