Numerical Methods/Numerical Differentiation

< Numerical Methods

Often in Physics or Engineering it is necessary to use a calculus operation known as differentiation. Unlike textbook mathematics, the differentiated functions are data generated by an experiment or a computer code.

Begin with the Taylor series as seen in Equation 1.

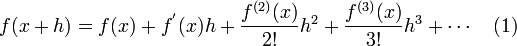
$f(x+h) = f(x) + f^{'}(x)h + \frac{f^{(2)}(x)}{2!}h^{2}+\frac{f^{(3)}(x)}{3!}h^{3}+ \cdots \quad (1)$

Next by cutting off the Taylor series after the fourth term and evaluating it at h and -h yields Equations (2) and (3).

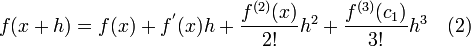
$f(x+h) = f(x) + f^{'}(x)h + \frac{f^{(2)}(x)}{2!}h^{2} +\frac{f^{(3)}(c_{1})}{3!}h^{3} \quad (2)$

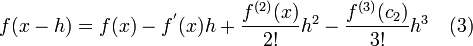
$f(x-h) = f(x) - f^{'}(x)h + \frac{f^{(2)}(x)}{2!}h^{2} - \frac{f^{(3)}(c_{2})}{3!}h^{3} \quad (3)$

Then by subtracting Equation (2) by Equation (3) yields.

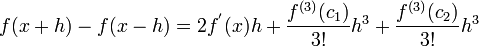
$f(x+h) - f(x-h) = 2f^{'}(x)h + \frac{f^{(3)}(c_{1})}{3!}h^{3} + \frac{f^{(3)}(c_{2})}{3!}h^{3}$

Central Difference

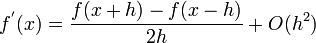
$f^{'}(x) = \frac{f(x+h)-f(x-h)}{2h} + O(h^{2})$

Forward Difference

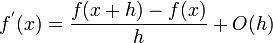
$f^{'}(x) = \frac{f(x+h)-f(x)}{h} + O(h)$

Backward Difference

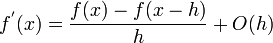
$f^{'}(x) = \frac{f(x)-f(x-h)}{h} + O(h)$

Second Derivative

The second order derivatives can be obtained by adding equations (2) and (3) (if properly expanded to include the fourth-derivative-term):

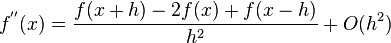
$f^{''}(x) = \frac{f(x+h)-2f(x)+f(x-h)}{h^2} + O(h^2)$

This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.