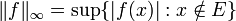Measure Theory/L^p spaces
< Measure TheoryRecall that an  space is defined as
space is defined as 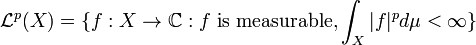
Jensen's inequality
Let  be a probability measure space.
be a probability measure space.
Let 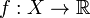 ,
, 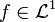 be such that there exist
be such that there exist 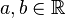 with
with 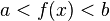
If 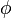 is a convex function on
is a convex function on 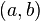 then,
then,
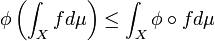
Proof
Let 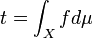 . As
. As 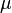 is a probability measure,
is a probability measure, 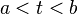
Let 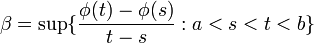
Let 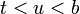 ; then
; then 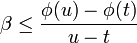
Thus, 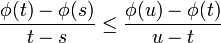 , that is
, that is 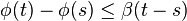
Put 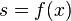
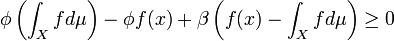 , which completes the proof.
, which completes the proof.
Corollary
- Putting
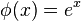 ,
,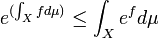
- If
 is finite,
is finite, 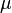 is a counting measure, and if
is a counting measure, and if 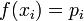 , then
, then 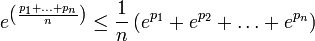
For every 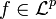 , define
, define 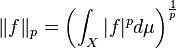
Holder's inequality
Let 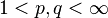 such that
such that 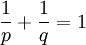 . Let
. Let 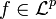 and
and 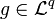 .
.
Then, 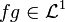 and
and
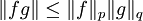
Proof
We know that 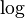 is a concave function
is a concave function
Let 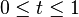 ,
, 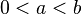 . Then
. Then 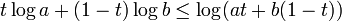
That is, 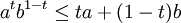
Let 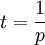 ,
, 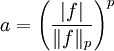 ,
, 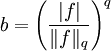
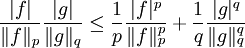
Then, 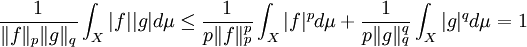 ,
,
which proves the result
Corollary
If 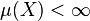 ,
,  then
then 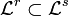
Proof
Let 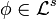 ,
, 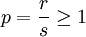 ,
, 
Then, 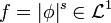 , and hence
, and hence 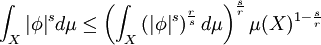
We say that if 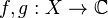 ,
,  almost everywhere on
almost everywhere on 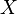 if
if 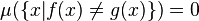 . Observe that this is an equivalence relation on
. Observe that this is an equivalence relation on 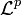
If 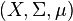 is a measure space, define the space
is a measure space, define the space 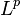 to be the set of all equivalence classes of functions in
to be the set of all equivalence classes of functions in 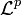
Theorem
The 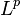 space with the
space with the 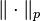 norm is a normed linear space, that is,
norm is a normed linear space, that is,
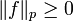 for every
for every 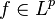 , further,
, further, 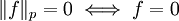
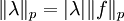
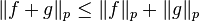 . . . (Minkowski's inequality)
. . . (Minkowski's inequality)
Proof
1. and 2. are clear, so we prove only 3. The cases  and
and  (see below) are obvious, so assume that
(see below) are obvious, so assume that 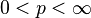 and let
and let 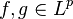 be given. Hölder's inequality yields the following, where
be given. Hölder's inequality yields the following, where 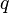 is chosen such that
is chosen such that 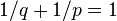 so that
so that 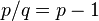 :
:
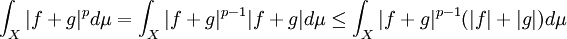
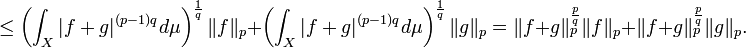
Moreover, as  is convex for
is convex for 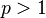 ,
,
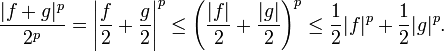
This shows that 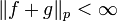 so that we may divide by it in the previous calculation to obtain
so that we may divide by it in the previous calculation to obtain 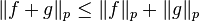 .
.
Define the space 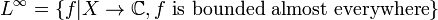 . Further, for
. Further, for 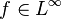 define
define