Measure Theory/Integration
< Measure TheoryLet 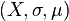 be a
be a 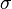 -finite measure space. Suppose
-finite measure space. Suppose  is a positive simple measurable function, with
is a positive simple measurable function, with 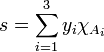 ;
; 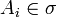 are disjoint.
are disjoint.
Define 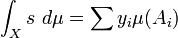
Let 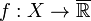 be measurable, and let
be measurable, and let 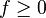 .
.
Define 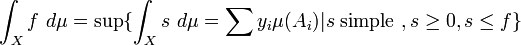
Now let 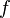 be any measurable function. We say that
be any measurable function. We say that 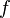 is integrable if
is integrable if 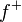 and
and 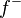 are integrable and if
are integrable and if 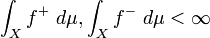 . Then, we write
. Then, we write
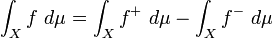
The class of measurable functions on  is denoted by
is denoted by 
For 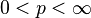 , we define
, we define 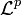 to be the collection of all measurable functions
to be the collection of all measurable functions 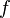 such that
such that 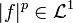
A property is said to hold almost everywhere if the set of all points where the property does not hold has measure zero.
Properties
Let 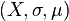 be a measure space and let
be a measure space and let 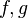 be measurable on
be measurable on 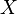 . Then
. Then
- If
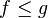 , then
, then 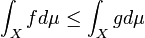
- If
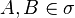 ,
, 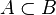 , then
, then 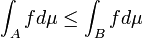
- If
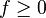 and
and 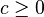 then
then 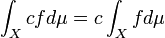
- If
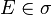 ,
, 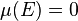 , then
, then 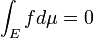 , even if
, even if 
- If
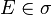 ,
, 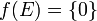 , then
, then 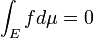 , even if
, even if 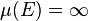
Proof
Monotone Convergence Theorem
Suppose 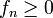 and
and 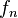 are measurable for all
are measurable for all 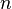 such that
such that
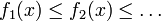 for every
for every 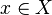
 almost everywhere on
almost everywhere on 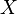
Then, 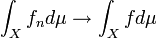
Proof
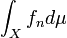 is an increasing sequence in
is an increasing sequence in  , and hence,
, and hence, 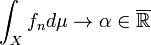 (say). We know that
(say). We know that 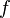 is measurable and that
is measurable and that 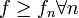 . That is,
. That is,
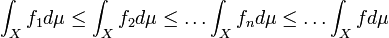
Hence, 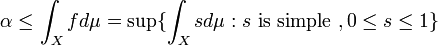
Let ![c\in [0,1]](../I/m/6ea0a95f41192a6ad436a6874796e0cb.png)
Define 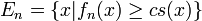 ;
; 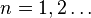 . Observe that
. Observe that 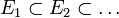 and
and 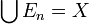
Suppose 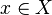 . If
. If 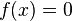 then
then 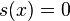 implying that
implying that 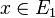 . If
. If 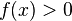 , then there exists
, then there exists 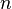 such that
such that 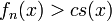 and hence,
and hence, 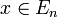 .
.
Thus, 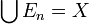 , therefore
, therefore 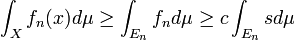 . As this is true if
. As this is true if ![c\in [0,1]](../I/m/6ea0a95f41192a6ad436a6874796e0cb.png) , we have that
, we have that 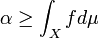 . Thus,
. Thus, 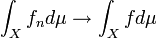 .
.
Fatou's Lemma
Let 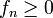 be measurable functions. Then,
be measurable functions. Then,
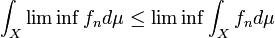
Proof
For 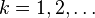 define
define 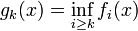 . Observe that
. Observe that 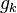 are measurable and increasing for all
are measurable and increasing for all 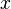 .
.
As  ,
, 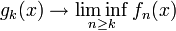 . By monotone convergence theorem,
. By monotone convergence theorem,
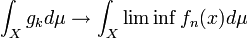 and as
and as 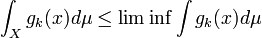 , we have the result.
, we have the result.
Dominated convergence theorem
Let 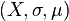 be a complex measure space. Let
be a complex measure space. Let 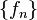 be a sequence of complex measurable functions that converge pointwise to
be a sequence of complex measurable functions that converge pointwise to 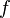 ;
; 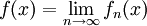 , with
, with 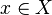
Suppose  for some
for some 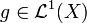 then
then
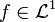 and
and 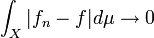 as
as 
Proof
We know that 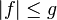 and hence
and hence 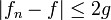 , that is,
, that is, 
Therefore, by Fatou's lemma, 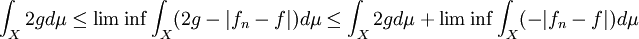
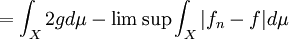
As 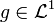 ,
, 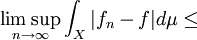 implying that
implying that 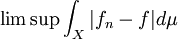
Theorem
- Suppose
![f:X\to[0,\infty]](../I/m/2fb58d8cc01c5a0e217aedffdc6507b3.png) is measurable,
is measurable, 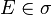 with
with 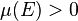 such that
such that 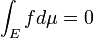 . Then
. Then 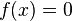 almost everywhere
almost everywhere 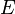
- Let
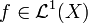 and let
and let 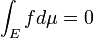 for every
for every 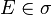 . Then,
. Then,  almost everywhere on
almost everywhere on 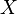
- Let
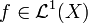 and
and 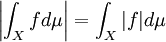 then there exists constant
then there exists constant 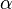 such that
such that 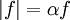 almost everywhere on
almost everywhere on 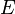
Proof
- For each
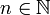 define
define 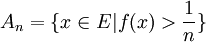 . Observe that
. Observe that 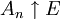
but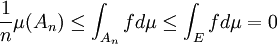 Thus
Thus 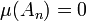 for all
for all 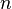 , by continuity,
, by continuity,  almost everywhere on
almost everywhere on 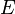
- Write
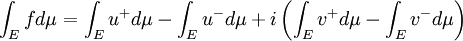 , where
, where 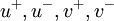 are non-negative real measurable.
are non-negative real measurable.
Further as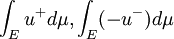 are both non-negative, each of them is zero. Thus, by applying part I, we have that
are both non-negative, each of them is zero. Thus, by applying part I, we have that 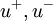 vanish almost everywhere on
vanish almost everywhere on 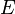 . We can similarly show that
. We can similarly show that 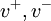 vanish almost everywhere on
vanish almost everywhere on 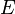 .
.