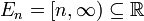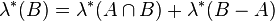Measure Theory/Basic Structures And Definitions/Measures

< Measure Theory < Basic Structures And Definitions

In this section, we study measure spaces and measures.

Measure Spaces

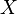Let $X$ be a set and $\mathcal{M}$ be a collection of subsets of $X$ such that 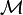$\mathcal{M}$ is a σ-ring.

We call the pair 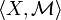$\left\langle X,\mathcal{M}\right\rangle$ a measure space. Members of 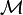$\mathcal{M}$ are called measurable sets.

A positive real valued function 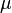$\mu$ defined on 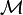$\mathcal{M}$ is said to be a measure if and only if,

(i)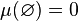 $\mu (\varnothing)=0$ and

(i)"Countable additivity": 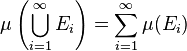$\mu\left(\bigcup_{i=1}^\infty E_i\right) = \sum_{i=1}^\infty \mu(E_i)$ , where 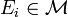$E_i\in\mathcal{M}$ are pairwise disjoint sets.

we call the triplet 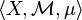$\left\langle X,\mathcal{M},\mu\right\rangle$ a measurable space

A probability measure is a measure with total measure one (i.e., μ(X)=1); a probability space is a measure space with a probability measure.

Properties

Several further properties can be derived from the definition of a countably additive measure.

Monotonicity

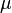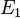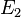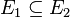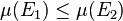$\mu$ is monotonic: If $E_1$ and $E_2$ are measurable sets with $E_1\subseteq E_2$ then $\mu(E_1) \leq \mu(E_2)$ .

Measures of infinite unions of measurable sets

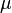$\mu$ is subadditive: If 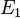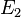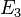$E_1$ , $E_2$ , $E_3$ , ... is a countable sequence of sets in $\Sigma$ , not necessarily disjoint, then

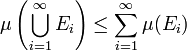\mu\left( \bigcup_{i=1}^\infty E_i\right) \le \sum_{i=1}^\infty \mu(E_i)

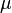$\mu$ is continuous from below: If 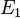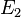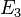$E_1$ , $E_2$ , $E_3$ , ... are measurable sets and 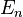$E_n$ is a subset of 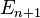$E_{n+1}$ for all n, then the union of the sets 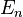$E_n$ is measurable, and

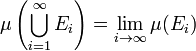\mu\left(\bigcup_{i=1}^\infty E_i\right) = \lim_{i\to\infty} \mu(E_i)

Measures of infinite intersections of measurable sets

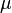$\mu$ is continuous from above: If 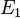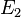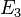$E_1$ , $E_2$ , $E_3$ , ... are measurable sets and 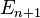$E_{n+1}$ is a subset of 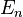$E_n$ for all n, then the intersection of the sets 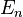$E_n$ is measurable; furthermore, if at least one of the 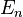$E_n$ has finite measure, then

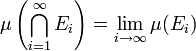\mu\left(\bigcap_{i=1}^\infty E_i\right) = \lim_{i\to\infty} \mu(E_i)

This property is false without the assumption that at least one of the 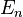$E_n$ has finite measure. For instance, for each n ∈ N, let

E_n = [n, \infty) \subseteq \mathbb{R}

which all have infinite measure, but the intersection is empty.

Counting Measure

Start with a set Ω and consider the sigma algebra X on Ω consisting of all subsets of Ω. Define a measure μ on this sigma algebra by setting μ(A) = |A| if A is a finite subset of Ω and μ(A) = ∞ if A is an infinite subset of Ω, where |A| denotes the cardinality of set A. Then (Ω, X, μ) is a measure space. μ is called the counting measure.

Lebesgue Measure

For any subset B of Rⁿ, we can define an outer measure 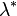$\lambda^*$ by:

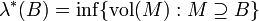\lambda^*(B) = \inf \{\operatorname{vol}(M) : M \supseteq B \}

, and

M \

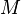is a countable union of products of intervals .

Here, vol(M) is sum of the product of the lengths of the involved intervals. We then define the set A to be Lebesgue measurable if

\lambda^*(B) = \lambda^*(A \cap B) + \lambda^*(B - A)

for all sets B. These Lebesgue measurable sets form a σ-algebra, and the Lebesgue measure is defined by λ(A) = λ^*(A) for any Lebesgue measurable set A.

This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.