Inorganic Chemistry/Chemical Bonding/VSEPR theory
< Inorganic Chemistry < Chemical BondingHistory
The idea of a correlation between molecular geometry and number of valence electrons (both shared and unshared) was first presented in a Bakerian Lecture in 1940 by Nevil Sidgwick and Herbert Powell at the University of Oxford.[1] In 1957 Ronald Gillespie and Ronald Sydney Nyholm at University College London refined this concept to build a more detailed theory capable of choosing between various alternative geometries.[2][3]
Overview
The VSEPR rules mainly involve predicting the layout of electron pairs surrounding one or more central atoms in a molecule, which are bonded to two or more other atoms. The geometry of these central atoms in turn determines the geometry of the larger whole.
The number of electron pairs in the valence shell of a central atom is determined by drawing the Lewis structure of the molecule, expanded to show all lone pairs of electrons as well as electron-pair bonds. Where two or more resonance structures can depict a molecule, the VSEPR model is applicable to any such structure. In VSEPR theory, a double bond or triple bond are treated as a single bonding group.[4]
These electron pairs (or groups if multiple bonds are present) are assumed to lie on the surface of a sphere centered on the central atom, and since they are negatively charged, tend to occupy positions that minimizes their mutual electrostatic repulsions by maximizing the distance between them. The number of electron pairs, therefore, determine the overall geometry that they will adopt.
For example, when there are two electron pairs surrounding the central atom, their mutual repulsion is minimal when they lie at opposite poles of the sphere. Therefore, the central atom is predicted to adopt a linear geometry. If there are 3 electron pairs surrounding the central atom, their repulsion is minimized by placing them at the vertices of an equilateral triangle centered on the atom. Therefore, the predicted geometry is trigonal. Likewise, for 4 electron pairs, the optimal arrangement is tetrahedral.
Degree of repulsion
The overall geometry is further refined by distinguishing between bonding and nonbonding electron pairs. The bonding electron pair shared in a sigma bond with an adjacent atom lies further from the central atom than a nonbonding (lone) pair of that atom, which is held close to its positively-charged nucleus. VSEPR theory therefore views repulsion by the lone pair to be greater than the repulsion by a bonding pair. As such, when a molecule has 2 interactions with different degrees of repulsion, VSEPR theory predicts the structure where lone pairs occupy positions that allow them to experience less repulsion. Lone pair-lone pair (lp-lp) repulsions are considered stronger than lone pair-bonding pair (lp-bp) repulsions, which in turn are considered stronger than bonding pair-bonding pair (bp-bp) repulsions, distinctions that then guide decisions about overall geometry when 2 or more non-equivalent positions are possible.[4] For instance, when 5 ligands or lone pairs surround a central atom, a trigonal bipyramidal molecular geometry is specified. In this geometry, the 2 collinear "axial" positions lie 180° apart from one another, and 90° from each of 3 adjacent "equatorial" positions; these 3 equatorial positions lie 120° apart from each other and experience only two closer proximity 90° neighbors (the axial positions). The axial positions therefore experience more repulsion than the equatorial positions; hence, when there are lone pairs, they tend to occupy equatorial positions.[5]
The difference between lone pairs and bonding pairs may also be used to rationalize deviations from idealized geometries. For example, the H2O molecule has four electron pairs in its valence shell: two lone pairs and two bond pairs. The four electron pairs are spread so as to point roughly towards the apices of a tetrahedron. However, the bond angle between the two O-H bonds is only 104.5°, rather than the 109.5° of a regular tetrahedron, because the two lone pairs (whose density or probability envelopes lie closer to the oxygen nucleus) exert a greater mutual repulsion than the two bond pairs.[4][5]
An advanced-level explanation replaces the above distinction with two rules:
- Bent's rule: An electron pair of a more electropositive ligand constitutes greater repulsion. This explains why the Cl in PClF4 prefers the equatorial position and why the bond angle in oxygen difluoride (103.8°) is smaller than that of water (104.5°). Lone pairs are then considered to be a special case of this rule, held by a "ghost ligand" in the limit of electropositivity.
- A higher bond order constitutes greater repulsion. This explains why in phosgene, the oxygen-chlorine bond angle (124.1°) is larger than the chlorine-chlorine bond angle (111.8°) even though chlorine is more electropositive than oxygen. In the carbonate ion, all three bond angles are equivalent due to resonance.
AXE method
The "AXE method" of electron counting is commonly used when applying the VSEPR theory. The A represents the central atom and always has an implied subscript one. The X represents the number of sigma bonds between the central atoms and outside atoms. Multiple covalent bonds (double, triple, etc.) count as one X. The E represents the number of lone electron pairs surrounding the central atom. The sum of X and E is known as the steric number.
Based on the steric number and distribution of X's and E's, VSEPR theory makes the predictions in the following tables. Note that the geometries are named according to the atomic positions only and not the electron arrangement. For example the description of AX2E1 as bent means that AX2 is a bent molecule without reference to the lone pair, although the lone pair helps to determine the geometry.
| Steric No. |
Basic geometry 0 lone pair |
1 lone pair | 2 lone pairs | 3 lone pairs |
|---|---|---|---|---|
| 2 | | |||
| 3 |  |  | ||
| 4 | 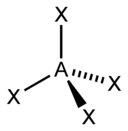 | 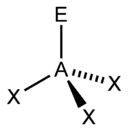 |  | |
| 5 | 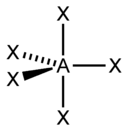 | 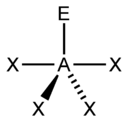 |  |  |
| 6 |  |  |  | |
| 7 | 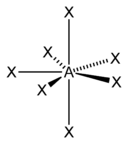 |  |  | |
| 8 | (IF−8) | | ||
| 9 | Tricapped trigonal prismatic (ReH2−9) OR Capped square antiprismatic |
| Molecule Type | Shape | Electron arrangement† | Geometry‡ | Examples |
|---|---|---|---|---|
| AX2E0 | Linear | |
|
BeCl2, HgCl2, CO2 |
| AX2E1 | Bent |  |
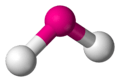 |
NO−2, SO2, O3, CCl2 |
| AX2E2 | Bent |  |
 |
H2O, OF2 |
| AX2E3 | Linear | 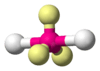 |
|
XeF2, I−3, XeCl2 |
| AX3E0 | Trigonal planar | 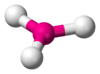 |
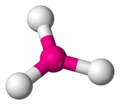 |
BF3, CO2−3, NO−3, SO3 |
| AX3E1 | Trigonal pyramidal | 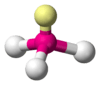 |
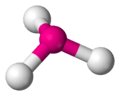 |
NH3, PCl3 |
| AX3E2 | T-shaped | 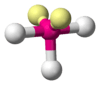 |
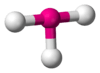 |
ClF3, BrF3 |
| AX4E0 | Tetrahedral | 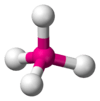 |
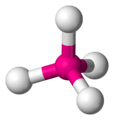 |
CH4, PO3−4, SO2−4, ClO−4, TiCl4, XeO4 |
| AX4E1 | Seesaw |  |
 |
SF4 |
| AX4E2 | Square planar | 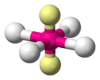 |
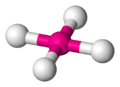 |
XeF4 |
| AX5E0 | Trigonal bipyramidal | 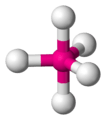 |
 |
PCl5 |
| AX5E1 | Square pyramidal | 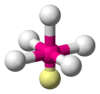 |
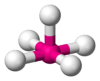 |
ClF5, BrF5, XeOF4 |
| AX5E2 | Pentagonal planar | 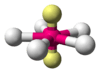 |
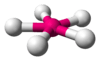 |
XeF−5 |
| AX6E0 | Octahedral | 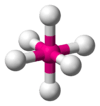 |
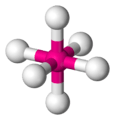 |
SF6, WCl6 |
| AX6E1 | Pentagonal pyramidal |  |
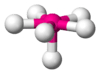 |
XeOF−5, IOF2−5 [6] |
| AX7E0 | Pentagonal bipyramidal | 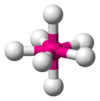 |
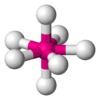 |
IF7 |
| AX8E0 | Square antiprismatic |  |
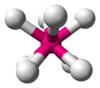 |
IF−8, ZrF4−8, ReF−8 |
| AX9E0 | Tricapped trigonal prismatic OR capped square antiprismatic |
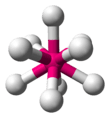 |
 |
ReH2−9 |
When the substituent (X) atoms are not all the same, the geometry is still approximately valid, but the bond angles may be slightly different from the ones where all the outside atoms are the same. For example, the double-bond carbons in alkenes like C2H4 are AX3E0, but the bond angles are not all exactly 120°. Likewise, SOCl2 is AX3E1, but because the X substituents are not identical, the XAX angles are not all equal.
As a tool in predicting the geometry adopted with a given number of electron pairs, an often used physical demonstration of the principle of minimal electrostatic repulsion utilizes inflated balloons. Through handling, balloons acquire a slight surface electrostatic charge that results in the adoption of roughly the same geometries when they are tied together at their stems as the corresponding number of electron pairs. For example, five balloons tied together adopt the trigonal bipyramidal geometry, just as do the five bonding pairs of a PCl5 molecule (AX5) or the two bonding and three non-bonding pairs of a XeF2 molecule (AX2E3). The molecular geometry of the former is also trigonal bipyramidal, whereas that of the latter is linear.
Examples
The methane molecule (CH4) is tetrahedral because there are four pairs of electrons. The four hydrogen atoms are positioned at the vertices of a tetrahedron, and the bond angle is cos−1(−1⁄3) ≈ 109°28'.[7] This is referred to as an AX4 type of molecule. As mentioned above, A represents the central atom and X represents all of the outer atoms.
The ammonia molecule (NH3) has three pairs of electrons involved in bonding, but there is a lone pair of electrons on the nitrogen atom. It is not bonded with another atom; however, it influences the overall shape through repulsions. As in methane above, there are four regions of electron density. Therefore, the overall orientation of the regions of electron density is tetrahedral. On the other hand, there are only three outer atoms. This is referred to as an AX3E type molecule because the lone pair is represented by an E. The observed shape of the molecule is a trigonal pyramid, because the lone pair is not "visible" in experimental methods used to determine molecular geometry. The shape of a molecule is found from the relationship of the atoms even though it can be influenced by lone pairs of electrons.
A steric number of seven or greater is possible, but it occurs in uncommon compounds such as iodine heptafluoride (IF7). The base geometry for a steric number of 7 is pentagonal bipyramidal.
The most common geometry for a steric number of eight is a square antiprismatic geometry.[8] Examples of this include the octacyanomolybdate (Mo(CN)4−8) and octafluorozirconate (ZrF4−8) anions.[8]
The nonahydridorhenate ion (ReH2−9) in potassium nonahydridorhenate is a rare example of a compound with a steric number of nine, which has a tricapped trigonal prismatic geometry.[9][10] Another example is the octafluoroxenate ion (XeF2−8) in nitrosonium octafluoroxenate(VI),[11][12] although in this case one of the electron pairs is a lone pair, and therefore the molecule actually has a distorted square antiprismatic geometry.
Possible geometries for steric numbers of 10, 11, or 12 are bicapped square antiprismatic, octadecahedral, and icosahedral, respectively. No compounds with steric numbers this high involving monodentate ligands exist, and those involving multidentate ligands can often be analysed more simply as complexes with lower steric numbers when some multidentate ligands are treated as a unit.[13]
Exceptions
There are groups of compounds where VSEPR fails to predict the correct geometry.
Some AX2E0 molecules
The gas phase structures of the triatomic halides of the heavier members of group 2, (i.e., calcium, strontium and barium halides, MX2), are not linear as predicted but are bent, (approximate X-M-X angles: CaF2, 145°; SrF2, 120°; BaF2, 108°; SrCl2, 130°; BaCl2, 115°; BaBr2, 115°; BaI2, 105°).[14] It has been proposed by Gillespie that this is caused by interaction of the ligands with the electron core of the metal atom, polarising it so that the inner shell is not spherically symmetric, thus influencing the molecular geometry.[15][16] Disilynes are also bent, despite having no lone pairs.[citation needed]
Some AX2E2 molecules
One example is molecular lithium oxide, Li2O, which is linear rather than being bent, and this has been ascribed to the bonding's being in essence ionic, leading to strong repulsion between the lithium atoms.[17]
Another example is O(SiH3)2 with an Si-O-Si angle of 144.1°, which compares to the angles in Cl2O (110.9°), (CH3)2O (111.7°)and N(CH3)3 (110.9°). Gillespie's rationalisation is that the localisation of the lone pairs, and therefore their ability to repel other electron pairs, is greatest when the ligand has an electronegativity similar to, or greater than, that of the central atom.[15] When the central atom is more electronegative, as in O(SiH3)2, the lone pairs are less well-localised and have a weaker repulsive effect. This fact, combined with the stronger ligand-ligand repulsion (-SiH3 is a relatively large ligand compared to the examples above), gives the larger-than-expected Si-O-Si bond angle.[15]
Some AX6E1 and AX8E1 molecules

Some AX6E1 molecules, e.g. xenon hexafluoride (XeF6) and the Te(IV) and Bi(III) anions, TeCl2−6, TeBr2−6, BiCl3−6, BiBr3−6 and BiI3−6, are octahedra rather than pentagonal pyramids, and the lone pair does not affect the geometry to the degree predicted by VSEPR.[18] One rationalization is that steric crowding of the ligands allows no room for the non-bonding lone pair;[15] another rationalization is the inert pair effect.[19]
Transition metal molecules
Many transition metal compounds have unusual geometries, which can be ascribed to absence of valence shell lone pairs and ligand bonding interaction with the d subshell.[20] Gillespie suggested that this interaction can be weak or strong. Weak interaction results in the same shapes as their main group analogues, while strong interaction produces bonding pairs that also occupy the respective antipodal points of the sphere.[21] This is similar to predictions based on sd hybrid orbitals[22][23] using the VALBOND theory. The repulsion of these bidirectional bonding pairs leads to a different prediction of shapes.
| Molecule Type | Shape[24] | Geometry‡[24] | Examples |
|---|---|---|---|
| AX2 | Bent |  |
VO2+ |
| AX3 | Trigonal pyramidal |  |
CrO3 |
| AX4 | Tetrahedral |  |
TiCl4 |
| AX5 | Square pyramidal |  |
Ta(CH3)5[25] |
| AX6 | Trigonal prismatic | 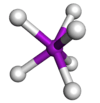 |
W(CH3)6 |
An anomaly is that a d8 electronic configuration in addition to weak ligand interaction results in a square planar shape. This can be rationalized by considering the increased crystal field stabilization energy as compared to a tetrahedral geometry.
Odd-electron molecules
The VSEPR theory can be extended to molecules with an odd number of electrons by treating the unpaired electron as a "half electron pair". In effect, the odd electron has an influence on the geometry which is similar to a full electron pair, but less pronounced so that the geometry may be intermediate between the molecule with a full electron pair and the molecule with one less electron pair on the central atom.
For example, nitrogen dioxide (NO2) is an AX2E0.5 molecule, with an unpaired electron on the central nitrogen. VSEPR predicts a geometry similar to the NO−2 ion (AX2E1, bent, bond angle approx. 120°) but intermediate between NO−2 and NO+2 (AX2E0, linear, 180°). In fact NO2 is bent with an angle of 134° which is closer to 120° than to 180°, in qualitative agreement with the theory.
Similarly chlorine dioxide (ClO2, AX2E1.5) has a geometry similar to ClO−2 but intermediate between ClO−2 and ClO+2.
Finally the methyl radical (CH3) is predicted to be trigonal pyramidal like the methyl anion (CH−3) but with a larger bond angle as in the trigonal planar methyl cation (CH+3). However in this case the VSEPR prediction is not quite true as CH3 is actually planar, although its distortion to a pyramidal geometry requires very little energy.[26]
VSEPR and orbital hybridisation
The VSEPR theory is frequently taught in conjunction with orbital hybridisation as the two give similar predictions. However, the two are unrelated as the former is based on the Pauli exclusion principle while the latter is based on the Schrödinger equation. The key difference between the VSEPR theory and orbital hybridisation is that the latter includes bonding interactions; in this respect, the relationship between the two can be compared to that between crystal field theory and ligand field theory.
References
- ↑ http://rspa.royalsocietypublishing.org/content/176/965/153.abstract N.V.Sidgwick and H.M.Powell, Proc.Roy.Soc.A 176, 153–180 (1940) Bakerian Lecture. Stereochemical Types and Valency Groups
- ↑ R.J.Gillespie and R.S.Nyholm, Quart.Rev. 11, 339 (1957)
- ↑ R.J.Gillespie, J.Chem.Educ. 47, 18(1970)
- 1 2 3
- 1 2
- ↑ Template:Cite doi
- ↑ "Angle Between 2 Legs of a Tetrahedron" – Maze5.net
- 1 2 Wiberg, Egon (2001). Inorganic Chemistry. Arnold Frederick Holleman. Academic Press. p. 1165. ISBN 0-12-352651-5.
- ↑ Holleman, A. F.; Wiberg, E. "Inorganic Chemistry" Academic Press: San Diego, 2001. ISBN 0-12-352651-5.
- ↑ Housecroft, C.E. and Sharpe A.G. "Inorganic Chemistry" (2nd edn, Pearson 2005. ISBN 0130-39913-2), p.254
- ↑ Template:Cite doi
- ↑ Hanson, Robert M. (1995). Molecular origami: precision scale models from paper. University Science Books. ISBN 0-935702-30-X.
- ↑ Template:Holleman&Wiberg
- ↑ Template:Greenwood&Earnshaw
- 1 2 3 4 Models of molecular geometry, Gillespie R. J., Robinson E.A. Chem. Soc. Rev., 2005, 34, 396–407, doi: 10.1039/b405359c
- ↑ Core Distortions and Geometries of the Difluorides and Dihydrides of Ca, Sr, and Ba Bytheway I, Gillespie R.J, Tang T.H., Bader R.F. Inorganic Chemistry, 34,9, 2407–2414, 1995 doi:10.1021/ic00113a023
- ↑ A spectroscopic determination of the bond length of the LiOLi molecule: Strong ionic bonding, D. Bellert, W. H. Breckenridge, J. Chem. Phys. 114, 2871 (2001); doi:10.1063/1.1349424
- ↑ Wells A.F. (1984) Structural Inorganic Chemistry 5th edition Oxford Science Publications ISBN 0-19-855370-6
- ↑ Template:Housecroft2nd
- ↑ Kaupp, Martin (2001). ""Non-VSEPR" Structures and Bonding in d(0) Systems". Angew Chem Int Ed Engl. 40 (1): 3534–3565. doi:10.1002/1521-3773(20011001)40:19<3534::AID-ANIE3534>3.0.CO;2-#.
- ↑ R. J. Gillespie (2008). "Fifty years of the VSEPR model". Coordination Chemistry Reviews 252: 1315–1327. doi:10.1016/j.ccr.2007.07.007.
- ↑ Landis, C. R.; Cleveland, T.; Firman, T. K. Making sense of the shapes of simple metal hydrides. J. Am. Chem. Soc. 1995, 117, 1859–1860.
- ↑ Landis, C. R.; Cleveland, T.; Firman, T. K. Structure of W(CH3)6. Science 1996, 272, 182–183.
- 1 2
- ↑ King, R. Bruce (2000). "Atomic orbitals, symmetry, and coordination polyhedra". Coordination Chemistry Reviews 197: 141–168.
- ↑ Anslyn E.V. and Dougherty D.A., Modern Physical Organic Chemistry (University Science Books, 2006), p.57