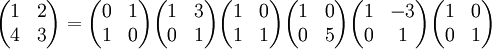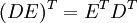High School Mathematics Extensions/Matrices/Project/Elementary Matrices

< High School Mathematics Extensions < Matrices < Project

Content
HSME
Matrices
Recurrence Relations
Problems & Projects
Problem Set
Project
Soultions
Exercises Solutions
Problem Set Solutions
Misc.
Definition Sheet
Full Version

Project -- Elementary matrices

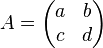
Throughout, $A = \begin{pmatrix}a & b\\ c & d\end{pmatrix}$

1. The matrices below are called elementary matrices. How are the matrices below different from the identity matrix I, describe each one.

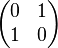
$\begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}$
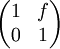$\begin{pmatrix} 1 & f \\ 0 & 1 \end{pmatrix}$ where f is a scalar
$\begin{pmatrix} 1 & 0 \\ f & 1 \end{pmatrix}$ where f is a scalar
$\begin{pmatrix} f & 0 \\ 0 & 1 \end{pmatrix}$ where f is a scalar
$\begin{pmatrix} 1 & 0 \\ 0 & f \end{pmatrix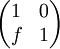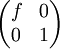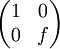}$ where f is a scalar

2. In each of the cases, compute B then describe how is B different from A

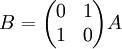
$B = \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}A$
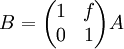$B = \begin{pmatrix} 1 & f \\ 0 & 1 \end{pmatrix}A$ where f is a scalar
$B = \begin{pmatrix} 1 & 0 \\ f & 1 \end{pmatrix}A$ where f is a scalar
$B = \begin{pmatrix} f & 0 \\ 0 & 1 \end{pmatrix}A$ where f is a scalar
$B = \begin{pmatrix} 1 & 0 \\ 0 & f \end{pmatrix}A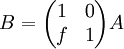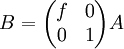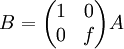$ where f is a scalar

3. The matrix 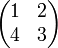$\begin{pmatrix}1 & 2\\4 & 3\end{pmatrix}$ has determinant not equal to zero. We can decompose the matrix into products of elementary matrices pre-multiplying the identity:

\begin{pmatrix}1 & 2\\4 & 3\end{pmatrix} = \begin{pmatrix}0 & 1\\1 & 0\end{pmatrix} \begin{pmatrix}1 & 3\\0 & 1\end{pmatrix} \begin{pmatrix}1 & 0\\1 & 1\end{pmatrix} \begin{pmatrix}1 & 0\\0 & 5\end{pmatrix} \begin{pmatrix}1 & -3\\0 & 1\end{pmatrix} \begin{pmatrix}1 & 0\\0 & 1\end{pmatrix}

Now suppose det(A) ≠ 0, can A be expressed as the product of elementary matrices and the identity?

4. a) Show that every elementary matrix has an inverse. Hint: use determinant.

b) Prove that every invertible matrix (a matrix that has an inverse) is the product of some elementary matrices pre-multiplying the identity.

5. A transpose of a matrix C is the matrix C^T where the ith row of C is the ith column of C^T. Prove using elementary matrices that

(DE)^T = E^TD^T

for arbitrary matrices D and E.

6. Show that every invertible matrix is also the product of some elementary matrices post-multiplying the identity.

7. How about non-invertible matrices? What can you say about them?

This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.