Geometry/Circles/Tangents and Secants

< Geometry < Circles

A tangent is a line in the same plane as a given circle that meets that circle in exactly one point. That point is called the point of tangency. A tangent cannot pass through a circle; if it does, it is classified as a chord. A secant is a line containing a chord.

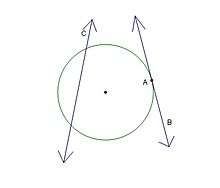
The point of tangency is labeled A, the tangent line is labeled B, and the secant line is labeled C.

A common tangent is a line tangent to two circles in the same plane. If the tangent does not intersect the line containing and connecting the centers of the circles, it is an external tangent. If it does, it is an internal tangent.

Two circles are tangent to one another if in a plane they intersect the same tangent in the same point.

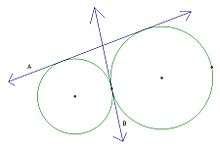
The external tangent is labeled A, and the internal tangent is labeled B.

This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.