Geometry/Angles

An angle is the union of two rays with a common endpoint, called the vertex. The angles formed by vertical and horizontal lines are called right angles; lines, segments, or rays that intersect in right angles are said to be perpendicular.

Angles, for our purposes, can be measured in either degrees (from 0 to 360) or radians (from 0 to ). Angles length can be determined by measuring along the arc they map out on a circle. In radians we consider the length of the arc of the circle mapped out by the angle. Since the circumference of a circle is , a right angle is radians. In degrees, the circle is 360 degrees, and so a right angle would be 90 degrees.

Naming Conventions

Angles are named in several ways.

• By naming the vertex of the angle (only if there is only one angle formed at that vertex; the name must be non-ambiguous)
• By naming a point on each side of the angle with the vertex in between.
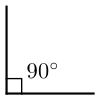
• By placing a small number on the interior of the angle near the vertex.

Hai

Classification of Angles by Degree Measure

Acute Angle

• an angle is said to be acute if it measures between 0 and 90 degrees, exclusive.

Right Angle

• an angle is said to be right if it measures 90 degrees.
• notice the small box placed in the corner of a right angle, unless the box is present it is not assumed the angle is 90 degrees.
• all right angles are congruent

Obtuse Angle

• an angle is said to be obtuse if it measures between 90 and 180 degrees, exclusive.

Special Pairs of Angles

• adjacent angles
  • adjacent angles are angles with a common vertex and a common side.
  • adjacent angles have no interior points in common.

• complementary angles
  • complementary angles are two angles whose sum is 90 degrees.
  • complementary angles may or may not be adjacent.
  • if two complementary angles are adjacent, then their exterior sides are perpendicular.
• supplementary angles
  • two angles are said to be supplementary if their sum is 180 degrees.
  • supplementary angles need not be adjacent.
  • if supplementary angles are adjacent, then the sides they do not share form a line.
• linear pair
  • if a pair of angles is both adjacent and supplementary, they are said to form a linear pair.
• vertical angles
  • angles with a common vertex whose sides form opposite rays are called vertical angles.
  • vertical angles are congruent.

Navigation

• Geometry
• Part I- Euclidean Geometry:
  • Chapter 1. Geometry/Points, Lines, Line Segments and Rays
  • Chapter 2. Geometry/Angles
  • Chapter 3. Geometry/Properties
  • Chapter 4. Geometry/Inductive and Deductive Reasoning
  • Chapter 5. Geometry/Proof
  • Chapter 6. Geometry/Five Postulates of Euclidean Geometry
  • Chapter 7. Geometry/Vertical Angles
  • Chapter 8. Geometry/Parallel and Perpendicular Lines and Planes
  • Chapter 9. Geometry/Congruency and Similarity
  • Chapter 10. Geometry/Congruent Triangles
  • Chapter 11. Geometry/Similar Triangles
  • Chapter 12. Geometry/Quadrilaterals
  • Chapter 13. Geometry/Parallelograms
  • Chapter 14. Geometry/Trapezoids
  • Chapter 15. Geometry/Circles/Radii, Chords and Diameters
  • Chapter 16. Geometry/Circles/Arcs
  • Chapter 17. Geometry/Circles/Tangents and Secants
  • Chapter 18. Geometry/Circles/Sectors
  • Appendix A. Geometry/Postulates & Definitions
  • Appendix B. Geometry/The SMSG Postulates for Euclidean Geometry

• Part II- Coordinate Geometry:
  • Geometry/Synthetic versus analytic geometry

• Two and Three-Dimensional Geometry and Other Geometric Figures
  • Geometry/Perimeter and Arclength
  • Geometry/Area
  • Geometry/Volume
  • Geometry/Polygons
  • Geometry/Triangles
  • Geometry/Right Triangles and Pythagorean Theorem
  • Geometry/Polyominoes
  • Geometry/Ellipses
  • Geometry/2-Dimensional Functions
  • Geometry/3-Dimensional Functions
  • Geometry/Area Shapes Extended into 3rd Dimension
  • Geometry/Area Shapes Extended into 3rd Dimension Linearly to a Line or Point
  • Geometry/Polyhedras
  • Geometry/Ellipsoids and Spheres
  • Geometry/Coordinate Systems (currently incorrectly linked to Astronomy)

• Traditional Geometry:
  • Geometry/Topology
  • Geometry/Erlanger Program
  • Geometry/Hyperbolic and Elliptic Geometry
  • Geometry/Affine Geometry
  • Geometry/Projective Geometry
  • Geometry/Neutral Geometry
  • Geometry/Inversive Geometry

• Modern geometry
  • Geometry/Algebraic Geometry
  • Geometry/Differential Geometry
  • Geometry/Algebraic Topology
  • Geometry/Noncommutative Geometry

• Geometry/An Alternative Way and Alternative Geometric Means of Calculating the Area of a Circle