General Relativity/Stoke's theorem

< General Relativity

Stokes' Theorem states that if there is an n-dimensional orientable manifold 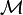$\mathcal{M}$ with boundary 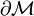$\partial\mathcal{M}$ , and if there is a form 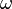$\omega$ (with compact support) defined on the manifold, then the following is true:

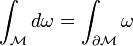
$\int_{\mathcal{M}}d\omega = \int_{\partial\mathcal{M}}\omega$

This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.