General Relativity/Rigorous Definition of Tensors

< General Relativity

We have seen that a 1-form ("covariant vector") can be thought of an operator with one slot in which we insert a vector ("contravariant vector") and get the scalar 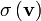$\mathbf{\sigma} \left( \mathbf{v} \right)$ . Similarly, a vector can be thought of as an operator with one slot in which we can insert a 1-form to obtain the scalar 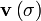$\mathbf{v} \left( \mathbf{\sigma} \right)$ . 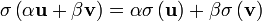As operators, they are linear, i.e., $\mathbf{\sigma} \left( \alpha \mathbf{u} +\beta \mathbf{v} \right) = \alpha \mathbf{\sigma} \left( \mathbf{u} \right) + \beta \mathbf{\sigma} \left( \mathbf{v} \right)$ .

A tensor of rank n is an operator with n slots for inserting vectors or 1-forms, which, when all n slots are filled, returns a scalar. In order for such an operator to be a tensor, it must be linear in each slot and obey certain transformation rules (more on this later). An example of a rank 2 tensor is 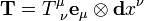$\mathbf{T} = T^\mu_{\ \nu} \mathbf{e}_\mu \otimes \mathbf{d}x^\nu$ . The symbol $\otimes$ (pronounced "tensor") tells you which slot each index acts on. 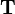This tensor $\mathbf{T}$ is said to be of type 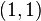$(1,1)$ because it has one contravariant slot and one covariant slot. Since 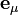$\mathbf{e}_\mu$ acts on the first slot and 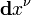$\mathbf{d}x^\nu$ acts on the second slot, we must insert a 1-form in the first slot and a vector in the second slot (remember, 1-forms act on vectors and vice-versa). 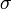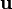Filling both of these slots, say with $\mathbf{\sigma}$ and $\mathbf{u}$ , will return the scalar 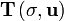$\mathbf{T} \left( \mathbf{\sigma}, \mathbf{u} \right)$ . We can use linearity (remember, the tensor is linear in each slot) to evaluate this number:

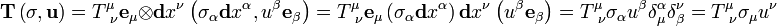
\mathbf{T} \left( \mathbf{\sigma}, \mathbf{u} \right) = T^\mu_{\ \nu} \mathbf{e}_\mu \otimes \mathbf{d}x^\nu \left( \sigma_\alpha \mathbf{d}x^\alpha, u^\beta \mathbf{e}_\beta \right) = T^\mu_{\ \nu} \mathbf{e}_\mu \left( \sigma_\alpha \mathbf{d}x^\alpha \right) \mathbf{d}x^\nu \left( u^\beta \mathbf{e}_\beta \right) = T^\mu_{\ \nu} \sigma_\alpha u^\beta \delta^\alpha_\mu \delta^\nu_\beta = T^\mu_{\ \nu} \sigma_\mu u^\nu

We don't have to fill all of the slots. This will of course not produce a scalar, but it will lower the rank of the tensor. For example, if we fill the second slot of 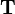$\mathbf{T}$ , but not the first, we get a rank 1 tensor of type 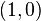$(1,0)$ (which is a contravariant vector):

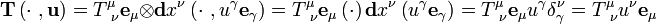
\mathbf{T} \left( \cdot \ , \mathbf{u} \right) = T^\mu_{\ \nu} \mathbf{e}_\mu \otimes \mathbf{d}x^\nu \left( \cdot \ , u^\gamma \mathbf{e}_\gamma \right) = T^\mu_{\ \nu} \mathbf{e}_\mu \left( \cdot \right) \mathbf{d}x^\nu \left( u^\gamma \mathbf{e}_\gamma \right) =T^\mu_{\ \nu} \mathbf{e}_\mu u^\gamma \delta^\nu_\gamma = T^\mu_{\ \nu} u^\nu \mathbf{e}_\mu

For another example, consider the rank 5 tensor 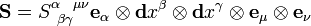$\mathbf{S}=S^{\alpha \ \ \mu \nu} _{\ \beta \gamma} \mathbf{e}_\alpha \otimes \mathbf{d}x^\beta \otimes \mathbf{d}x^\gamma \otimes \mathbf{e}_\mu \otimes \mathbf{e}_\nu$ . This is a tensor of type 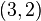$(3,2)$ . We can fill all of its slots to get a scalar:

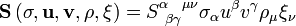
\mathbf{S} \left( \mathbf{\sigma}, \mathbf{u}, \mathbf{v}, \mathbf{\rho}, \mathbf{\xi} \right) = S^{\alpha \ \ \mu \nu} _{\ \beta \gamma} \sigma_\alpha u^\beta v^\gamma \rho_\mu \xi_\nu

Filling only the 3rd and 4th slots, we get a rank 3 tensor of type 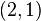$(2,1)$ :

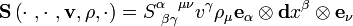
\mathbf{S} \left( \cdot \ , \cdot \ , \mathbf{v}, \mathbf{\rho}, \cdot \right) = S^{\alpha \ \ \mu \nu} _{\ \beta \gamma} v^\gamma \rho_\mu \mathbf{e}_\alpha \otimes \mathbf{d}x^\beta \otimes \mathbf{e}_\nu

As a final note, it should be mentioned that in General Relativity we will always have a special tensor called the "metric tensor" which will allow us to convert contravariant indices to covariant indices and vice-versa. This way, we can change the tensor type 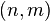$(n,m)$ and be able to insert either 1-forms or vectors into any slot of a given tensor.

This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.