General Relativity/Differentiable manifolds

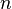A smooth $n$ -dimensional manifold 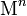$\mathrm{M}^n$ is a set together with a collection of subsets 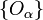$\{O_\alpha\}$ with the following properties:

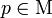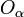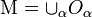Each $p\in\mathrm{M}$ lies in at least one $O_\alpha$ , that is $\mathrm{M}=\cup_\alpha O_\alpha$ .
For each 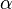$\alpha$ , there is a bijection 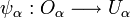$\psi_\alpha:O_\alpha\longrightarrow U_\alpha$ , where 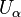$U_\alpha$ is an open subset of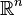 $\mathbb{R}^n$
If 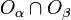$O_\alpha\cap O_\beta$ is non-empty, then the map $\psi_\alpha\circ\psi_\beta^{-1}:\psi_\beta[O_\alpha\cap O_\beta]\longrightarrow\psi_\alpha[O_\alpha\cap O_\beta]$ is smooth.

The bijections are called charts or coordinate systems. The collection of charts is called an atlas. The atlas induces a topology on M such that the charts are continuous. The domains 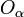$O_\alpha$ of the charts are called coordinate regions.

Examples

Euclidean space, 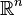$\mathbb{R}^n$ with a single chart ( 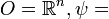$O=\mathbb{R}^n,\psi=$ identity map) is a trivial example of a manifold.
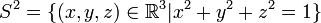2-sphere $S^2 = \{ (x,y,z) \in \mathbb{R}^3 | x^2 + y^2 + z^2 = 1 \}$ .

Notice that

S^2

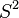is not an open subset of

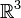\mathbb{R}^3

. The identity map on

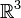\mathbb{R}^3

restricted to

S^2

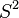does not satisfy the requirements of a chart since its range is not open in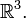

\mathbb{R}^3.

The usual spherical coordinates map

S^2

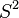to a region in

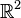\mathbb{R}^2

, but again the range is not open in

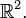\mathbb{R}^2.

Instead, one can define two charts each defined on a subset of

S^2

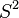that omits a half-circle. If these two half-circles do not intersect, the union of the domains of the two charts is all of

S^2

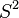. With these two charts,

S^2

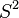becomes a 2-dimensional manifold. It can be shown that no single chart can possibly cover all of

S^2

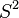if the topology of

S^2

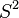is to be the usual one.

This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.