Fundamentals of Transportation/Traffic Signals/Solution

< Fundamentals of Transportation < Traffic Signals

Problem:

An approach at a pretimed signalized intersection has an arrival rate of 500 veh/hr and a saturation flow rate of 3000 veh/hr. 30 seconds of effective green are given in a 100-second cycle. Analyze the intersection assuming D/D/1 queueing by describing the proportion of the cycle with a queue, the maximum number of vehicles in the queue, the total and average delay, and the maximum delay.

Solution:

With the statements in the problem, we know:

Green Time = 30 seconds
Red Time = 70 seconds
Cycle Length = 100 seconds
Arrival Rate = 500 veh/hr (0.138 veh/sec)
Departure Rate = 3000 veh/hr (0.833 veh/sec)

Traffic intensity, 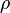$\rho$ , is the first value to calculate.

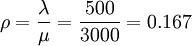
$\rho = \frac{{\lambda}}{{\mu}} = \frac{{500}}{{3000}} = 0.167\,\!$

Time to queue clearance after the start of effective green:

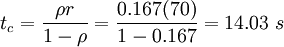
$t_c {\rm{ }} = {\rm{ }}\frac{{\rho r}}{{1 - \rho }} = \frac{{0.167(70)}}{{1 - 0.167}} = 14.03\ s \,\!$

Proportion of the cycle with a queue:

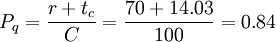
$P_q {\rm{ }} = {\rm{ }}\frac{{r{\rm{ }} + {\rm{ }}t_c }}{C}{\rm{ }} = {\rm{ }}\frac{{70{\rm{ }} + {\rm{ }}14.03 }}{100}{\rm{ }} = 0.84\,\!$

Proportion of vehicles stopped:

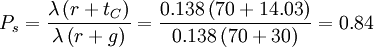
$P_s = \frac{{\lambda \left( {r + t_C } \right)}}{{\lambda \left( {r + g} \right)}} = \frac{{0.138 \left( {70 + 14.03 } \right)}}{{0.138 \left( {70 + 30} \right)}} = 0.84 \,\!$

Maximum number of vehicles in the queue:

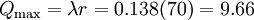
$Q_{\max } {\rm{ }} = {\rm{ }}\lambda r = {\rm{ }}0.138(70) = 9.66 \,\!$

Total vehicle delay per cycle:

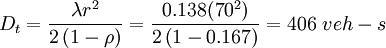
$D_t {\rm{ }} = {\rm{ }}\frac{{\lambda r^2 }}{{2\left( {1 - \rho } \right)}}{\rm{ }} = {\rm{ }}\frac{{0.138(70^2) }}{{2\left( {1 - 0.167 } \right)}}{\rm{ }} = 406\ veh-s \,\!$

Average delay per vehicle:

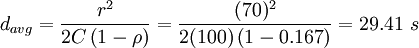
$d_{avg} {\rm{ }} = \frac{{r^2 }}{{2C\left( {1 - \rho } \right)}} = \frac{{(70)^2 }}{{2(100)\left( {1 - 0.167} \right)}} = 29.41\ s\,\!$

Maximum delay of any vehicle:

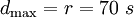
$d_{\max } {\rm{ }} = {\rm{ }}r = {\rm{ }} 70\ s \,\!$

Thus, the solution can be determined:

Proportion of the cycle with a queue = 0.84
Maximum number of vehicles in the queue = 9.66
Total Delay = 406 veh-sec
Average Delay = 29.41 sec
Maximum Delay = 70 sec

This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.