Fundamentals of Transportation/Traffic

< Fundamentals of Transportation

Almost anybody can build a road. Its safety and durability would likely come into question if done by an amateur, but roads are not a difficult thing to deploy. Management of these roads, however, is something that is far from simple. Safety, efficiency, and sensibility are all elements that come into play when managing a road. It is seldom possible to find a managing strategy that satisfies all three of these categories, but often a "good" strategy can be found by balancing tradeoffs. This section introduces the fundamentals of traffic management and operation, discussing everything from queueing theory to traffic signals. The discussions here cover the fundamentals for traffic operations. To this day, research is still being conducted to perfect these elements.

Queueing

Queueing is the study of traffic behavior near a certain section where demand exceeds available capacity. Queues can be seen in a variety of situations and transportation systems. Its presence is one of the causes of driver delay.

Traffic Flow

Traffic Flow is the study of the movement of individual drivers and vehicles between two points and the interactions they make with one another. While traffic flow cannot be predicted with one-hundred percent certainty due to unpredictable driver behavior, drivers tend to behave within a reasonable range that can be represented mathematically. Relationships have been established between the three main traffic flow characteristics:

Flow
Density
Velocity

Queueing and Traffic Flow

Queueing and Traffic Flow is the study of traffic flow behaviors surrounding queueing events. They merge concepts learned in the prior two sections and apply them to bottlenecks.

Shockwaves

Shockwaves are the byproducts of traffic congestion and queueing. They are defined as transition zones between two traffic states that are dynamic, meaning they generally have the ability to move. Most drivers can identify shockwaves as the propagation of brake lights stemming from a given incident.

Traffic Signals

Traffic Signals are one of the more familiar types of traffic control. Using either a fixed or adaptive schedule, traffic signals allow certain parts of the intersection to move while forcing other parts to wait, delivering instructions to drivers through a set of colorful lights. While many benefits come with traffic signals, they also come with a series of costs, such as increasing delay during the off-peak. But, traffic signals are generally a well-accepted form of traffic control for busy intersections and continue to be deployed.

Additional Areas of Study

Level of Service

One of the basic assessments of roadway performance is by determining its Level of Service (LOS). These Levels of Service, typically ranging between A and F (A being good performance, F being poor performance), are assessed by certain predetermined thresholds for any of the three characteristics of traffic flow (flow, density, and/or velocity). Finding the correct LOS often requires reference to a table.

When computing a value of flow to determine LOS, the following formula is used:

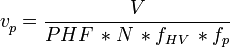
$v_p^{} = \frac{V}{{PHF\,*N\,*f_{HV} \,*f_p }}\,\!$

Where:

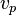$v_p$ = Actual Volume per Lane
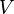$V$ = Hourly Volume
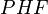$PHF$ = Peak Hour Factor
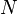$N$ = Number of Lanes
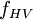$f_{HV}$ = Heavy Vehicle Factor
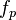$f_p$ = Driver Familiarity Factor (generally, a value of 1 for commuters, less for out-of-town drivers)

Peak Hour Factor is found to be:

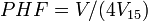
$PHF = V/(4V_{15}) \,\!$

Where:

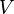$V$ = Hourly Volume
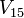$V_{15}$ = Peak 15-Minute Flow

The Heavy Vehicle Factor is found to be:

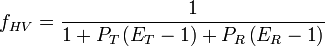
$f_{HV} = \frac{1}{{1 + P_T \left( {E_T - 1} \right) + P_R \left( {E_R - 1} \right)}}\,\!$

Where:

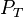$P_T$ = Percentage of Trucks, in decimal
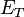$E_T$ = Passenger Car Equivalent of Trucks (found through table)
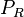$P_R$ = Percentage of Recreational Vehicles, in decimal
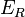$E_R$ = Passenger car Equivalent of Recreational Vehicles (found through table)

Similarly, LOS can be analyzed the anticipated speed of the corridor. The equation below produces the estimated free-flow speed for a strip of rural road, given certain characteristics about it:

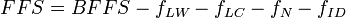
$FFS = BFFS - f_{LW} - f_{LC} - f_N - f_{ID}\,\!$

Where:

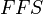$FFS$ = Estimated Free Flow Speed
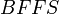$BFFS$ = Base Free Flow Speed
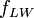$f_{LW}$ = Adjustment for Lane Width (found in tables)
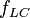$f_{LC}$ = Adjustment for Lateral Clearance (found in tables)
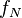$f_N$ = Adjustment for Number of Lanes (found in tables)
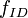$f_{ID}$ = Adjustment for Interchange Density (found in tables)

For multilane urban highways, free-flow speed is computed with a similar equation:

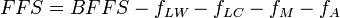
$FFS = BFFS - f_{LW} - f_{LC} - f_M - f_A\,\!$

Where:

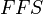$FFS$ = Estimated Free Flow Speed
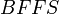$BFFS$ = Base Free Flow Speed
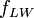$f_{LW}$ = Adjustment for Lane Width (found in tables)
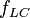$f_{LC}$ = Adjustment for Lateral Clearance (found in tables)
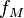$f_M$ = Adjustment for Median Type (found in tables)
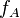$f_{A}$ = Adjustment for Access Points (found in tables)

Lateral Clearance is computed:

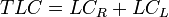
$TLC = LC_R + LC_L\,\!$

Where:

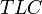$TLC$ = Total Lateral Clearance
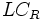$LC_R$ = Lateral Clearance on the Right Side of the Travel Lanes to Obstructions
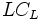$LC_L$ = Lateral Clearance on the Left Side of the Travel Lanes to Obstructions

Once TLC is computed, a table can provide the value for the Lateral Clearance Adjustment.

Estimating Gaps

One area of transportation operations that is still being considered is the estimation of gaps between vehicles. This is applicable in a variety of situations, primarily dealing with arrivals of vehicles at a given intersection. Gaps can only be predicted through a probability, based on several known characteristics occurring at a given time or location.

One of the more popular models used for predicting arrivals is the Poisson Model. This model is shown here:

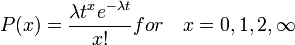
$P(x) = \frac{{\lambda t^x e^{ - \lambda t} }}{{x!}}for\quad x = 0,1,2,\infty \,\!$

Where:

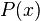$P(x)$ = Probability of having x vehicles arrive in time t
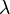$\lambda$ = Average vehicle flow or arrival rate
$t$ = Duration of the time interval over which vehicles are counted
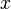$x$ = Number of vehicles to arrive in time t

Additional Questions

Variables

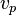$v_p$ - Actual Volume per Lane
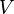$V$ - Hourly Volume
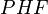$PHF$ - Peak Hour Factor
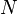$N$ - Number of Lanes
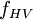$f_{HV}$ - Heavy Vehicle Factor
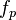$f_p$ - Driver Familiarity Factor (generally, a value of 1 for commuters, less for out-of-town drivers)
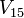$V_{15}$ - Peak 15-Minute Flow
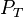$P_T$ - Percentage of Trucks, in decimal
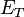$E_T$ - Passenger Car Equivalent of Trucks (found through table)
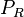$P_R$ - Percentage of Recreational Vehicles, in decimal
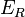$E_R$ - Passenger car Equivalent of Recreational Vehicles (found through table)
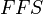$FFS$ - Estimated Free Flow Speed
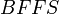$BFFS$ - Base Free Flow Speed
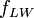$f_{LW}$ - Adjustment for Lane Width (found in tables)
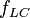$f_{LC}$ - Adjustment for Lateral Clearance (found in tables)
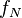$f_N$ - Adjustment for Number of Lanes (found in tables)
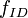$f_{ID}$ - Adjustment for Interchange Density (found in tables)
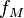$f_M$ - Adjustment for Median Type (found in tables)
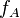$f_{A}$ - Adjustment for Access Points (found in tables)
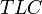$TLC$ - Total Lateral Clearance
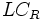$LC_R$ - Lateral Clearance on the Right Side of the Travel Lanes to Obstructions
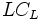$LC_L$ - Lateral Clearance on the Left Side of the Travel Lanes to Obstructions
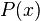$P(x)$ - Probability of having x vehicles arrive in time t
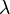$\lambda$ - Average vehicle flow or arrival rate
$t$ - Duration of the time interval over which vehicles are counted
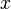$x$ - Number of vehicles to arrive in time t

References

This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.