Fundamentals of Transportation/Route Choice/Solution

< Fundamentals of Transportation < Route Choice

Problem:

Given a flow of six (6) units from origin “o” to destination “r”. Flow on each route ab is designated with Qab in the Time Function. Apply Wardrop's Network Equilibrium Principle (Users Equalize Travel Times on all used routes)

A. What is the flow and travel time on each link? (complete the table below) for Network A

Link Attributes
Link	Link Performance Function	Flow	Time
o-p	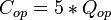$C_{op} = 5 *Q_{op}$
p-r	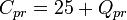$C_{pr} = 25 + Q_{pr}$
o-q	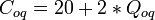$C_{oq} = 20 + 2*Q_{oq}$
q-r	$C_{qr} = 5 *Q_{qr}$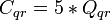

B. What is the system optimal assignment?

C. What is the Price of Anarchy?

Solution:

Part A

What is the flow and travel time on each link? Complete the table below for Network A:

Link Attributes
Link	Link Performance Function	Flow	Time
o-p	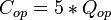$C_{op} = 5 *Q_{op}$
p-r	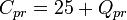$C_{pr} = 25 + Q_{pr}$
o-q	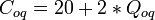$C_{oq} = 20 + 2*Q_{oq}$
q-r	$C_{qr} = 5 *Q_{qr}$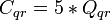

These four links are really 2 links O-P-R and O-Q-R, because by conservation of flow Qop = Qpr and Qoq = Qqr.

Link Attributes
Link	Link Performance Function	Flow	Time
o-p-r	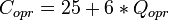$C_{opr} =25+ 6 *Q_{opr}$
o-q-r	$C_{oqr} = 20 + 7*Q_{oqr}$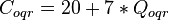

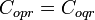By Wardrop's Equilibrium Principle, the travel time (cost) on each used route must be equal. Therefore $C_{opr} = C_{oqr}$ .

$25+ 6*Q_{opr}= 20+7*Q_{oqr}$

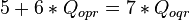
$5+ 6*Q_{opr}= 7*Q_{oqr}$

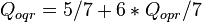
$Q_{oqr} = 5/7 + 6*Q_{opr}/7$

By the conservation of flow principle

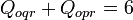
$Q_{oqr}+Q_{opr} = 6$

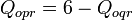
$Q_{opr} = 6 - Q_{oqr}$

By substitution

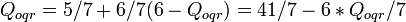
$Q_{oqr} = 5/7 + 6/7 (6 - Q_{oqr}) = 41/7 -6*Q_{oqr}/7$

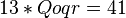
$13*Qoqr = 41$

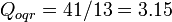
$Q_{oqr} = 41/13 = 3.15$

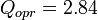
$Q_{opr}=2.84$

Check

$42.01 = 25+6(2.84)$

$42.05 = 20+7(3.15)$

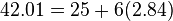
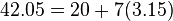
Check (within rounding error)

Link Attributes
Link	Link Performance Function	Flow	Time
o-p-r	$C_{opr} =25+ 6 *Q_{opr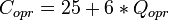}$	2.84	42.01
o-q-r	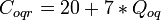$C_{oqr} = 20 + 7*Q_{oq}$	3.15	42.01

or expanding back to the original table:

Link Attributes
Link	Link Performance Function	Flow	Time
o-p	$C_{op} = 5 *Q_{op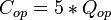}$	2.84	14.2
p-r	$C_{pr} = 25 + Q_{pr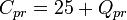}$	2.84	27.84
o-q	$C_{oq} = 20 + 2*Q_{oq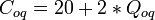}$	3.15	26.3
q-r	$C_{qr} = 5 *Q_{qr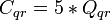}$	3.15	15.75

User Equilibrium: Total Delay = 42.01 * 6 = 252.06

Part B

What is the system optimal assignment?

Conservation of Flow:

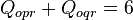
$Q_{opr}+Q_{oqr} = 6 \,\!$

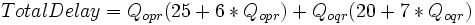
$Total Delay = Q_{opr}(25+ 6*Q_{opr}) + Q_{oqr}(20+7*Q_{oqr}) \,\!$

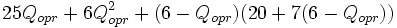
$25 Q_{opr} + 6 Q_{opr}^2 + (6-Q_{opr})( 20 + 7(6-Q_{opr}))\,\!$

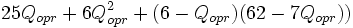
$25 Q_{opr} + 6 Q_{opr}^2 + (6-Q_{opr})( 62 - 7Q_{opr}))\,\!$

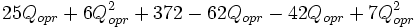
$25 Q_{opr} + 6 Q_{opr}^2 + 372 - 62 Q_{opr} - 42 Q_{opr} + 7 Q_{opr}^2\,\!$

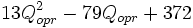
$13 Q_{opr}^2 - 79 Q_{opr} + 372\,\!$

Analytic Solution requires minimizing total delay

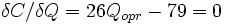
$\delta C/\delta Q = 26 Q_{opr} - 79 = 0\,\!$

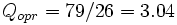
$Q_{opr} = 79/26 = 3.04\,\!$

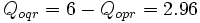
$Q_{oqr} = 6-Q_{opr}=2.96\,\!$

And we can compute the SO travel times on each path

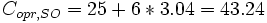
$C_{opr,SO} = 25+ 6*3.04 = 43.24 \,\!$

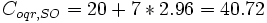
$C_{oqr,SO} = 20+7*2.96 = 40.72 \,\!$

Note that unlike the UE solution, 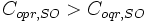$C_{opr,SO} > C_{oqr,SO} \,\!$

Total Delay = 3.04(25+ 6*3.04) + 2.96(20+7*2.96) = 131.45+120.53= 251.98

Note: one could also use software such as a "Solver" algorithm to find this solution.

Part C

What is the Price of Anarchy?

User Equilibrium: Total Delay =252.06 System Optimal: Total Delay = 251.98

Price of Anarchy = 252.06/251.98 = 1.0003 < 4/3

This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.