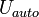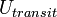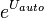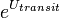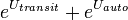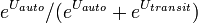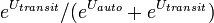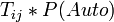Fundamentals of Transportation/Mode Choice/Solution
< Fundamentals of Transportation < Mode ChoiceProblem:
You are given the following mode choice model.
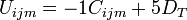
Where:
-
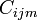 = travel cost between
= travel cost between 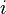 and
and 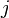 by mode
by mode 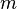
-
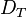 = dummy variable (alternative specific constant) for transit
= dummy variable (alternative specific constant) for transit
| Origin\Destination | Dakotopolis | New Fargo |
|---|---|---|
| Dakotopolis | 5 | 7 |
| New Fargo | 7 | 5 |
| Origin\Destination | Dakotopolis | New Fargo |
|---|---|---|
| Dakotopolis | 10 | 15 |
| New Fargo | 15 | 8 |
Solution:
Part A
A. Using a logit model, determine the probability of a traveler driving.
Solution Steps
- Compute Utility for Each Mode for Each Cell
- Compute Exponentiated Utilities for Each Cell
- Sum Exponentiated Utilities
- Compute Probability for Each Mode for Each Cell
- Multiply Probability in Each Cell by Number of Trips in Each Cell
| Origin\Destination | Dakotopolis | New Fargo |
|---|---|---|
| Dakotopolis | -5 | -7 |
| New Fargo | -7 | -5 |
| Origin\Destination | Dakotopolis | New Fargo |
|---|---|---|
| Dakotopolis | -5 | -10 |
| New Fargo | -10 | -3 |
| Origin\Destination | Dakotopolis | New Fargo |
|---|---|---|
| Dakotopolis | 0.0067 | 0.0009 |
| New Fargo | 0.0009 | 0.0067 |
| Origin\Destination | Dakotopolis | New Fargo |
|---|---|---|
| Dakotopolis | 0.0067 | 0.0000454 |
| New Fargo | 0.0000454 | 0.0565 |
| Origin\Destination | Dakotopolis | New Fargo |
|---|---|---|
| Dakotopolis | 0.0134 | 0.0009454 |
| New Fargo | 0.0009454 | 0.0498 |
| Origin\Destination | Dakotopolis | New Fargo |
|---|---|---|
| Dakotopolis | 0.5 | 0.953 |
| New Fargo | 0.953 | 0.12 |
| Origin\Destination | Dakotopolis | New Fargo |
|---|---|---|
| Dakotopolis | 0.5 | 0.047 |
| New Fargo | 0.047 | 0.88 |
Part B
B. Using the results from the previous problem (#2), how many car trips will there be?
Recall
| Origin\Destination | Dakotopolis | New Fargo |
|---|---|---|
| Dakotopolis | 9395 | 5606 |
| New Fargo | 6385 | 15665 |
| Origin\Destination | Dakotopolis | New Fargo |
|---|---|---|
| Dakotopolis | 4697 | 5339 |
| New Fargo | 6511 | 1867 |
This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.