Fractals/Rational

< Fractals

Herman ring - image with c++ src code

Iteration of complex rational functions^[1]^[2]^[3]

Examples

commons:Category:Complex rational maps
f(z)=z2/(z9-z+0,025) ^[4]
f(z)=(z3-z)/(dz2+1) where d=-0,003+0,995i ^[5]
f(z)=(z3-z)/(dz2+1) where d=1,001· e2Pi/30 ^[6]
Multibrot sets by Xender^[7]
$f_{\lambda }(z)=z^{n}+{\frac {\lambda }{z^{d}}}$ ^[8]

Rational functions
${\frac {z}{z-1}}$
${\frac {z^{2}}{z^{2}-1}}$
${\frac {z^{3}}{z^{3}-1}}$
${\frac {z^{4}}{z^{4}-1}}$
${\frac {z^{5}}{z^{5}-1}}$
${\frac {z^{7}}{z^{7}-1}}$

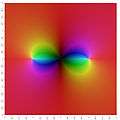
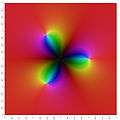
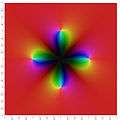
degree 6

Julia set of rational function f(z)=z^2(3 − z^4 ) over 2.png

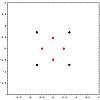
The Julia set of the degree 6 function f :^[9]

$f(z)=z^{2}{\frac {3-z^{4}}{2}}$

There are 3 superattracting fixed points at :

z = 0
z = 1
z = ∞

All other critical points are in the backward orbit of 1.

How to compute iteration :

z:x+y*%i;
z1:z^2*(3-z^4)/2;
realpart(z1);
((x^2−y^2)*(−y^4+6*x^2*y^2−x^4+3)−2*x*y*(4*x*y^3−4*x^3*y))/2
imagpart(z1);
(2*x*y*(−y^4+6*x^2*y^2−x^4+3)+(x^2−y^2)*(4*x*y^3−4*x^3*y))/2

Find fixed points using Maxima CAS :

z1:z^2*(3-z^4)/2;
s:solve(z1=z);
s:float(s);

result :

[z=−1.446857247913871,z=.7412709105660023,z=−1.357611535209976*%i−.1472068313260655,z=1.357611535209976*%i−.1472068313260655,z=1.0,z=0.0]

check multiplicities of the roots :

multiplicities;
[1,1,1,1,1,1]

 z1:z^2*(3-z^4)/2;
 s:solve(z1=z)$
 s:map(rhs,s)$
 f:z1;
 k:diff(f,z,1);
 define(d(z),k);
 m:map(d,s)$
 m:map(abs,m)$
 s:float(s);
 m:float(m);

Result : there are 6 fixed point 2 of them are supperattracting ( m=0 ), rest are repelling ( m>1 ):

 [−1.446857247913871,.7412709105660023,−1.357611535209976*%i−.1472068313260655,1.357611535209976*%i−.1472068313260655,1.0,0.0]
 [14.68114348748323,1.552374536603988,10.66447061028112,10.66447061028112,0.0,0.0]

Critical points :

[%i,−1.0,−1.0*%i,1.0,0.0]

References

This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.