Fractals/Mathematics/sequences

< Fractals < Mathematics

Definition

types of sequences

Integer sequences

Fraction sequences

Farey sequence

The Farey sequence of order n is the sequence of completely reduced vulgar fractions between 0 and 1 which when in lowest terms have denominators less than or equal to n, arranged in order of increasing size.

Each Farey sequence starts with the value 0, denoted by the fraction ⁰⁄₁, and ends with the value 1, denoted by the fraction ¹⁄₁ (although some authors omit these terms).

Farey Addition = the mediant of two fractions :

  ${\frac {a}{c}}\oplus {\frac {b}{d}}={\frac {a+b}{c+d}}$

Terms

next term = child
Previous terms = parents^[1]

Farey tree = Farey sequence as a tree

Sorted

 F1 = {0/1,                                                                                                          1/1}
 F2 = {0/1,                                                   1/2,                                                   1/1}
 F3 = {0/1,                               1/3,                1/2,                2/3,                               1/1}
 F4 = {0/1,                     1/4,      1/3,                1/2,                2/3,      3/4,                     1/1}
 F5 = {0/1,                1/5, 1/4,      1/3,      2/5,      1/2,      3/5,      2/3,      3/4, 4/5,                1/1}
 F6 = {0/1,           1/6, 1/5, 1/4,      1/3,      2/5,      1/2,      3/5,      2/3,      3/4, 4/5, 5/6,           1/1}
 F7 = {0/1,      1/7, 1/6, 1/5, 1/4, 2/7, 1/3,      2/5, 3/7, 1/2, 4/7, 3/5,      2/3, 5/7, 3/4, 4/5, 5/6, 6/7,      1/1}
 F8 = {0/1, 1/8, 1/7, 1/6, 1/5, 1/4, 2/7, 1/3, 3/8, 2/5, 3/7, 1/2, 4/7, 3/5, 5/8, 2/3, 5/7, 3/4, 4/5, 5/6, 6/7, 7/8, 1/1}

Sequences on the parameter plane

sequence from Siegel disk to Lea-Fatou flower

plain Siegel disk
digitated Siegel disk^[2]
virtual Siegel disk
? Leau-Fatou flower ?

Sharkovsky ordering

It is the infinite sequence of positive integers. It starts from 3 and ends in 1. It contains ininitely many subsequences.

"The Sharkovski ordering :

begins with the odd numbers >= 3,
then twice these numbers,
then 4 times them,
then 8 times them,
etc.,
ending with the powers of 2 in decreasing order, ending with 2^0 = 1."^[3]

sequence of fraction in the elephant valley

In the elephant valley^[4]^[5] ( from parameter plane ) there is a sequence of componts with period p : from 1/2 to 1/p

Note that :

internal ray 0/1 = 1/1
internal angle 1/p means that ray goes from period 1 component ( parent period = 1) to period p component ( child period = p)
as child period grows computations are harder
exponential growth^[6] of $2^{p}$ . One can easly create a numeric value that is too large to be represented within the available storage space ( integer overflow^[7] ). For example $2^{34}$ is to big for short ( 16 bit ) and long ( 32 bit) integer.

The upper principal sequence of rotational number around the main cardioid of Mandelbrot set^[8]

n	rotation number = 1/n	parameter c
2	1/2	-0.75
3	1/3	0.64951905283833*i-0.125
4	1/4	0.5*i+0.25
5	1/5	0.32858194507446*i+0.35676274578121
6	1/6	0.21650635094611*i+0.375
7	1/7	0.14718376318856*i+0.36737513441845
8	1/8	0.10355339059327*i+0.35355339059327
9	1/9	0.075191866590218*i+0.33961017714276
10	1/10	0.056128497072448*i+0.32725424859374

See :

Slide show of rescaled limbs converging to the Lavaurs elephant - video by Wolf Jung made with Mandel

sequence of fractions tending to the golden mean ( Golden Ratio Conjugate )

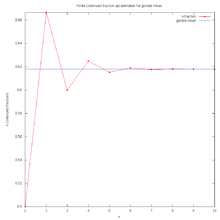
Approximations to the reciprocal golden ratio by finite continued fractions, or ratios of Fibonacci numbers

Golden Mean Quadratic Siegel Disc

n =   1 ;  p_n/q_n =  1.0000000000000000000 =                     1 /                    1 
n =   2 ;  p_n/q_n =  0.5000000000000000000 =                     1 /                    2 
n =   3 ;  p_n/q_n =  0.6666666666666666667 =                     2 /                    3 
n =   4 ;  p_n/q_n =  0.6000000000000000000 =                     3 /                    5 
n =   5 ;  p_n/q_n =  0.6250000000000000000 =                     5 /                    8 
n =   6 ;  p_n/q_n =  0.6153846153846153846 =                     8 /                   13 
n =   7 ;  p_n/q_n =  0.6190476190476190476 =                    13 /                   21 
n =   8 ;  p_n/q_n =  0.6176470588235294118 =                    21 /                   34 
n =   9 ;  p_n/q_n =  0.6181818181818181818 =                    34 /                   55 
n =  10 ;  p_n/q_n =  0.6179775280898876404 =                    55 /                   89 
n =  11 ;  p_n/q_n =  0.6180555555555555556 =                    89 /                  144 
n =  12 ;  p_n/q_n =  0.6180257510729613734 =                   144 /                  233 
n =  13 ;  p_n/q_n =  0.6180371352785145888 =                   233 /                  377 
n =  14 ;  p_n/q_n =  0.6180327868852459016 =                   377 /                  610 
n =  15 ;  p_n/q_n =  0.6180344478216818642 =                   610 /                  987 
n =  16 ;  p_n/q_n =  0.6180338134001252348 =                   987 /                 1597 
n =  17 ;  p_n/q_n =  0.6180340557275541796 =                  1597 /                 2584 
n =  18 ;  p_n/q_n =  0.6180339631667065295 =                  2584 /                 4181 
n =  19 ;  p_n/q_n =  0.6180339985218033999 =                  4181 /                 6765 
n =  20 ;  p_n/q_n =  0.6180339850173579390 =                  6765 /                10946 
n =  21 ;  p_n/q_n =  0.6180339901755970865 =                 10946 /                17711 
n =  22 ;  p_n/q_n =  0.6180339882053250515 =                 17711 /                28657 
n =  23 ;  p_n/q_n =  0.6180339889579020014 =                 28657 /                46368 
n =  24 ;  p_n/q_n =  0.6180339886704431856 =                 46368 /                75025 
n =  25 ;  p_n/q_n =  0.6180339887802426829 =                 75025 /               121393 
n =  26 ;  p_n/q_n =  0.6180339887383030068 =                121393 /               196418 
n =  27 ;  p_n/q_n =  0.6180339887543225376 =                196418 /               317811 
n =  28 ;  p_n/q_n =  0.6180339887482036214 =                317811 /               514229 
n =  29 ;  p_n/q_n =  0.6180339887505408394 =                514229 /               832040 
n =  30 ;  p_n/q_n =  0.6180339887496481015 =                832040 /              1346269 
n =  31 ;  p_n/q_n =  0.6180339887499890970 =               1346269 /              2178309 
n =  32 ;  p_n/q_n =  0.6180339887498588484 =               2178309 /              3524578 
n =  33 ;  p_n/q_n =  0.6180339887499085989 =               3524578 /              5702887 
n =  34 ;  p_n/q_n =  0.6180339887498895959 =               5702887 /              9227465 
n =  35 ;  p_n/q_n =  0.6180339887498968544 =               9227465 /             14930352 
n =  36 ;  p_n/q_n =  0.6180339887498940819 =              14930352 /             24157817 
n =  37 ;  p_n/q_n =  0.6180339887498951409 =              24157817 /             39088169 
n =  38 ;  p_n/q_n =  0.6180339887498947364 =              39088169 /             63245986 
n =  39 ;  p_n/q_n =  0.6180339887498948909 =              63245986 /            102334155 
n =  40 ;  p_n/q_n =  0.6180339887498948319 =             102334155 /            165580141 
n =  41 ;  p_n/q_n =  0.6180339887498948544 =             165580141 /            267914296 
n =  42 ;  p_n/q_n =  0.6180339887498948458 =             267914296 /            433494437 
n =  43 ;  p_n/q_n =  0.6180339887498948491 =             433494437 /            701408733 
n =  44 ;  p_n/q_n =  0.6180339887498948479 =             701408733 /           1134903170 
n =  45 ;  p_n/q_n =  0.6180339887498948483 =            1134903170 /           1836311903

This is a sequence of rational numbers ( Julia sets are parabolic). It's limit is an irrational number ( Julia set has a Siegel disk).

orbit
- period of the orbit

References

Hardy-DivergentSeries

This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.