Fractals/Iterations in the complex plane/r a directions

< Fractals < Iterations in the complex plane

Gallery

directions
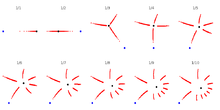critical orbits for internal angle from 1/1 to 1/10. True attracting directions
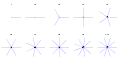Q-th arm stars for q from 1 to 10. Schematic directions
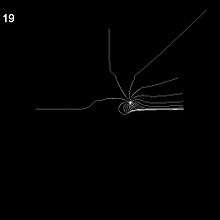True repelling directions : external rays that land on alfa fixed point for internal angle from 1/2 to 1/40

Class of functions : ^[1]

f(z)=z+mz^{k+1}+O(z^{k+2})

where :

Simplest subclass :

f(z)=z+mz^{k+1}

simplest example :

f(z)=z+z^{2}

W say that roots of unity, complex points v on unit circle $S^{1}=\{v:abs(v)=1\}$

\upsilon \in \partial \mathbb {D}

are attracting directions if :

{\frac {m}{|m|}}\upsilon ^{k}=-1

Critical orbit and directions for for complex quadratic polynomial and internal angle 1/3

On the complex z-plane ( dynamical plane) there are q directions described by angles:

$arg(z)=2\Pi {\frac {p}{q}}$

where :

$0\leq p<q$

Repelling and attracting directions ^[3]in turns near alfa fixed point for complex quadratic polynomials $f_{m}(z)=z^{2}+mz$

This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.