Fractals/Iterations in the complex plane/q-iterations

< Fractals < Iterations in the complex plane

Introduction

Julia set drawn by inverse iteration of critical orbit ( in case of Siegel disc )

Periodic external rays of dynamic plane made with backward iteration

Iteration in mathematics refer to the process of iterating a function i.e. applying a function repeatedly, using the output from one iteration as the input to the next.^[1] Iteration of apparently simple functions can produce complex behaviours and difficult problems.

applications

One can make inverse ( backward iteration) :

of repeller for drawing Julia set ( IIM/J)^[2]
of circle outside Jlia set (radius=ER) for drawing level curves of escape time ( which tend to Julia set)^[3]
of circle inside Julia set (radius=AR) for drawing level curves of attract time ( which tend to Julia set)^[4]
of critical orbit ( in Siegel disc case) for drawing Julia set ( probably only in case of Goldem Mean )
for drawing external ray

Repellor for forward iteration is attractor for backward iteration

Notes

Iteration is allways on the dynamic plane.
There is no dynamic on the parametr plane.
Mandelbrot set carries no dynamics. It is a set of parameter values.
There are no orbits on parameter plane, one should not draw orbits on parameter plane.
Orbit of critical point is on the dynamical plane

step

integer
fractional
Continuous Iteration of Dynamical Maps^[5]^[6]. This continuous iteration can be discretized by the finite element method and then solved—in parallel—on a computer.

decomposition

Move during iteration in case of complex quadratic polynomial is complex. It consists of 2 moves :

angular move = rotation ( see doubling map)
radial move ( see external and internal rays, invariant curves )
- fallin into target set and attractor ( in hyperbolic and parabolic case )

radial move
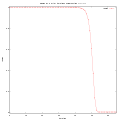Radius abs(z) = r < 1.0 after some iterations using f0(z) = z*z
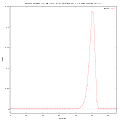Distance between repetive iteration of point smaller then one

angular move
angle 1/7 after doubling map
angle 1/15 after doubling map
angle 11/36 after doubling map

direction

backward

Backward iteration or inverse iteration

Peitgen

 /* Zn*Zn=Z(n+1)-c */
                Zx=Zx-Cx;
                Zy=Zy-Cy;
                /* sqrt of complex number algorithm from Peitgen, Jurgens, Saupe: Fractals for the classroom */
                if (Zx>0)
                {
                 NewZx=sqrt((Zx+sqrt(Zx*Zx+Zy*Zy))/2);
                 NewZy=Zy/(2*NewZx);        
                 }
                 else /* ZX <= 0 */
                 {
                  if (Zx<0)
                     {
                      NewZy=sign(Zy)*sqrt((-Zx+sqrt(Zx*Zx+Zy*Zy))/2);
                      NewZx=Zy/(2*NewZy);        
                      }
                      else /* Zx=0 */
                      {
                       NewZx=sqrt(fabs(Zy)/2);
                       if (NewZx>0) NewZy=Zy/(2*NewZx);
                          else NewZy=0;    
                      }
                 };
              if (rand()<(RAND_MAX/2))
              {   
                  Zx=NewZx;
                  Zy=NewZy; 
                  }
              else {Zx=-NewZx;
                  Zy=-NewZy; }

Mandel

Here is example of c code of inverse iteration using code from program Mandel by Wolf Jung

/*

 gcc i.c -lm -Wall
 ./a.out


iPeriodChild = 1 , c = (0.250000, 0.000000); z = (-0.0000000000000000, -0.5000000000000000) 
 iPeriodChild = 2 , c = (-0.750000, 0.000000); z = (-0.0000000000000001, 0.3406250193166067) z = 0.000000000000000  -0.340625019316607 i
 iPeriodChild = 3 , c = (-0.125000, 0.649519); z = (-0.2299551351162812, -0.1413579816050057) z = -0.229955135116281  -0.141357981605006 i
 iPeriodChild = 4 , c = (0.250000, 0.500000); z = (-0.2288905993372874, -0.0151096456992674) 
 iPeriodChild = 5 , c = (0.356763, 0.328582); z = (-0.1990400075391210, 0.0415980651776321) 
 iPeriodChild = 6 , c = (0.375000, 0.216506); z = (-0.1727194378627304, 0.0675726990190151) 
 iPeriodChild = 7 , c = (0.367375, 0.147184); z = (-0.1530209385352789, 0.0799609106267383) 
 iPeriodChild = 8 , c = (0.353553, 0.103553); z = (-0.1386555899358813, 0.0860089512209437) 
 iPeriodChild = 9 , c = (0.339610, 0.075192); z = (-0.1281114080080390, 0.0889429110652104) z = -0.128111408008039  +0.088942911065210 i


*/


#include <stdio.h>
#include <math.h> // M_PI; needs -lm also 
#include <complex.h>



/* find c in component of Mandelbrot set 
 
   uses code by Wolf Jung from program Mandel
   see function mndlbrot::bifurcate from mandelbrot.cpp
   http://www.mndynamics.com/indexp.html

*/
double complex GiveC(double InternalAngleInTurns, double InternalRadius, unsigned int Period)
{
  //0 <= InternalRay<= 1
  //0 <= InternalAngleInTurns <=1
  double t = InternalAngleInTurns *2*M_PI; // from turns to radians
  double R2 = InternalRadius * InternalRadius;
  double Cx, Cy; /* C = Cx+Cy*i */

  switch ( Period ) // of component 
    {
    case 1: // main cardioid
      Cx = (cos(t)*InternalRadius)/2-(cos(2*t)*R2)/4; 
      Cy = (sin(t)*InternalRadius)/2-(sin(2*t)*R2)/4; 
      break;
    case 2: // only one component 
      Cx = InternalRadius * 0.25*cos(t) - 1.0;
      Cy = InternalRadius * 0.25*sin(t); 
      break;
      // for each iPeriodChild  there are 2^(iPeriodChild-1) roots. 
    default: // higher periods : to do, use newton method 
      Cx = 0.0;
      Cy = 0.0; 
      break; }

  return Cx + Cy*I;
}





/* mndyncxmics::root from mndyncxmo.cpp  by Wolf Jung (C) 2007-2014. */

// input = x,y
// output = u+v*I = sqrt(x+y*i) 
complex double GiveRoot(complex double z)
{  
  double x = creal(z);
  double y = cimag(z);
  double u, v;
  
   v  = sqrt(x*x + y*y);

   if (x > 0.0)
        { u = sqrt(0.5*(v + x)); v = 0.5*y/u; return  u+v*I; }
   if (x < 0.0)
         { v = sqrt(0.5*(v - x)); if (y < 0.0) v = -v; u = 0.5*y/v; return  u+v*I; }
   if (y >= 0.0) 
       { u = sqrt(0.5*y); v = u; return  u+v*I; }


   u = sqrt(-0.5*y); 
   v = -u;
   return  u+v*I;
}



// from mndlbrot.cpp  by Wolf Jung (C) 2007-2014. part of Madel 5.12 
// input : c, z , mode
// c = cx+cy*i where cx and cy are global variables defined in mndynamo.h
// z = x+y*i
// 
// output : z = x+y*i
complex double InverseIteration(complex double z, complex double c)
{
    double x = creal(z);
    double y = cimag(z);
    double cx = creal(c);
    double cy = cimag(c);
   
   // f^{-1}(z) = inverse with principal value
   if (cx*cx + cy*cy < 1e-20) 
   {  
      z = GiveRoot(x - cx + (y - cy)*I); // 2-nd inverse function = key b 
      //if (mode & 1) { x = -x; y = -y; } // 1-st inverse function = key a   
      return -z;
   }
    
   //f^{-1}(z) =  inverse with argument adjusted
   double u, v;
   complex double uv ;
   double w = cx*cx + cy*cy;
    
   uv = GiveRoot(-cx/w -(cy/w)*I); 
   u = creal(uv);
   v = cimag(uv);
   //
   z =  GiveRoot(w - cx*x - cy*y + (cy*x - cx*y)*I);
   x = creal(z);
   y = cimag(z);
   //
   w = u*x - v*y; 
   y = u*y + v*x; 
   x = w;
  
   //if (mode & 1) // mode = -1
     //  { x = -x; y = -y; } // 1-st inverse function = key a
  
  return x+y*I; // key b =  2-nd inverse function 

}



// make iPeriod inverse iteration with negative sign ( a in Wolf Jung notation )
complex double GivePrecriticalA(complex double z, complex double c, int iPeriod)
{
  complex double za = z;  
  int i; 
  for(i=0;i<iPeriod ;++i){
    
    za = InverseIteration(za,c); 
    //printf("i = %d ,  z = (%f, %f) \n ", i,  creal(z), cimag(z) );

   }

 return za;
}

int main(){
  
 complex double c;
 complex double z;
 complex double zcr = 0.0; // critical point

 int iPeriodChild;
 int iPeriodChildMax = 10; // period of
 int iPeriodParent = 1; 
  
 



 for(iPeriodChild=1;iPeriodChild<iPeriodChildMax ;++iPeriodChild) {

     c = GiveC(1.0/((double) iPeriodChild), 1.0, iPeriodParent); // root point = The unique point on the boundary of a mu-atom of period P where two external angles of denominator = (2^P-1) meet.
     z = GivePrecriticalA( zcr, c, iPeriodChild);
     printf("iPeriodChild = %d , c = (%f, %f); z = (%.16f, %.16f) \n ", iPeriodChild, creal(c), cimag(c), creal(z), cimag(z) );
}





return 0; 
}

Test

One can iterate ad infinitum. Test tells when one can stop

bailout test for forward iteration

Target set or trap

Target set is used in test. When zn is inside target set then one can stop the iterations.

Planes

Parameter plane

"Mandelbrot set carries no dynamics. It is a set of parameter values. There are no orbits on parameter plane, one should not draw orbits on parameter plane. Orbit of critical point is on the dynamical plane"

Dynamic plane $f_{0}$ for c=0

Equipotential curves (in red) and integral curves (in blue) of a radial vector field with the potential function

\phi (x,y)={\sqrt {x^{2}+y^{2}}}

Lets take c=0, then one can call dynamical plane $f_{0}$ plane.

Here dynamical plane can be divided into :

Julia set = $\{z:|z|=1\}$
Fatou set which consists of 2 subsets :
- interior of Julia set = basin of attraction of finite attractor = $\{z:|z|<1\}$
- exterior of Julia set = basin of attraction of infinity = $\{z:|z|>1\}$

Forward iteration

The 10 first powers of a complex number inside the unit circle

Exponential spirals

Principle branch of arg

$z=re^{i\theta }\,$

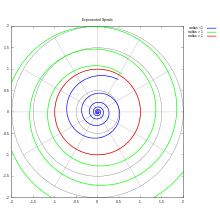
where :

r is the absolute value or modulus or magnitude of a complex number z = x + i
$\theta$ is the argument of complex number z (in many applications referred to as the "phase") is the angle of the radius with the positive real axis. Usually principal value is used

r=|z|={\sqrt {x^{2}+y^{2}}}.\,

\theta =\arg(z)=\operatorname {atan2} (y,x)={\begin{cases}\arctan({\frac {y}{x}})&{\mbox{if }}x>0\\\arctan({\frac {y}{x}})+\pi &{\mbox{if }}x<0{\mbox{ and }}y\geq 0\\\arctan({\frac {y}{x}})-\pi &{\mbox{if }}x<0{\mbox{ and }}y<0\\{\frac {\pi }{2}}&{\mbox{if }}x=0{\mbox{ and }}y>0\\-{\frac {\pi }{2}}&{\mbox{if }}x=0{\mbox{ and }}y<0\\{\mbox{indeterminate }}&{\mbox{if }}x=0{\mbox{ and }}y=0.\end{cases}}

$f_{0}(z)=z^{2}=(re^{i\theta })^{2}=r^{2}e^{i2\theta }\,$

and forward iteration :^[7]

$f_{0}^{n}(z)=r^{2^{n}}e^{i2^{n}\theta }\,$

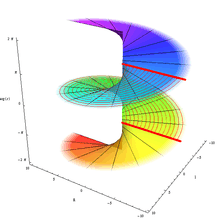
Forward iteration gives forward orbit = list of points {z0, z1, z2, z3... , zn} which lays on exponential spirals.^[8] ^[9]

Chaos and the complex squaring map

The informal reason why the iteration is chaotic is that the angle doubles on every iteration and doubling grows very quickly as the angle becomes ever larger, but angles which differ by multiples of 2π radians are identical. Thus, when the angle exceeds 2π, it must wrap to the remainder on division by 2π. Therefore, the angle is transformed according to the dyadic transformation (also known as the 2x mod 1 map). As the initial value z₀ has been chosen so that its argument is not a rational multiple of π, the forward orbit of z_n cannot repeat itself and become periodic.

More formally, the iteration can be written as:

\qquad z_{n+1}=z_{n}^{2}

where $z_{n}$ is the resulting sequence of complex numbers obtained by iterating the steps above, and $z_{0}$ represents the initial starting number. We can solve this iteration exactly:

\qquad z_{n}=z_{0}^{2^{n}}

Starting with angle θ, we can write the initial term as $z_{0}=\exp(i\theta )$ so that $z_{n}=\exp(i2^{n}\theta )$ . This makes the successive doubling of the angle clear. (This is equivalent to the relation $z_{n}=\cos(2^{n}\theta )+i\sin(2^{n}\theta )$ .)

Escape test

If distance between point z of exterior of Julia set and Julia set is :

 $distance(z,J_{c})=2^{-n}$

then point escapes ( measured using bailout test and escape time )

 $|z_{n}|>ER$

after :

$n$ steps in non-parabolic case
$2^{n}$ steps in parabolic case ^[10]

See here for the precision needed for escape test

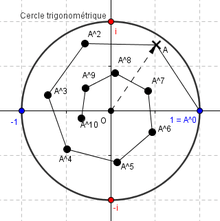
Backward iteration

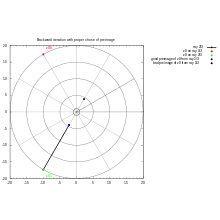
Backward iteration of complex quadratic polynomial with proper chose of the preimage

Every angle α ∈ R/Z measured in turns has :

one image = 2α mod 1 under doubling map
"two preimages under the doubling map: α/2 and (α + 1)/2." ^[11]. Inverse of doubling map is multivalued function.

Note that difference between these 2 preimages

{\frac {\alpha }{2}}-{\frac {\alpha +1}{2}}={\frac {1}{2}}

is half a turn = 180 degrees = Pi radians.

Images and preimages under doubling map d
$\alpha$	$d^{1}(\alpha )$	$d^{-1}(\alpha )$
${\frac {1}{2}}$	${\frac {1}{1}}$	$\left\{{\frac {1}{4}},{\frac {3}{4}}\right\}$
${\frac {1}{3}}$	${\frac {2}{3}}$	$\left\{{\frac {1}{6}},{\frac {4}{6}}\right\}$
${\frac {1}{4}}$	${\frac {1}{2}}$	$\left\{{\frac {1}{8}},{\frac {5}{8}}\right\}$
${\frac {1}{5}}$	${\frac {2}{5}}$	$\left\{{\frac {1}{10}},{\frac {6}{10}}\right\}$
${\frac {1}{6}}$	${\frac {1}{3}}$	$\left\{{\frac {1}{12}},{\frac {7}{12}}\right\}$
${\frac {1}{7}}$	${\frac {2}{7}}$	$\left\{{\frac {1}{14}},{\frac {4}{7}}\right\}$

On complex dynamical plane backward iteration using quadratic polynomial $f_{c}$

f_{c}(z)=z^{2}+c

gives backward orbit = binary tree of preimages :

$z\,$

$-{\sqrt {z-c}},+{\sqrt {z-c}}\,$

$-{\sqrt {-{\sqrt {z-c}}-c}},+{\sqrt {-{\sqrt {z-c}}-c}},-{\sqrt {+{\sqrt {z-c}}-c}},+{\sqrt {+{\sqrt {z-c}}-c}}\,$

One can't choose good path in such tree without extra informations.

Not that preimages show rotational symmetry ( 180 degrees)

For other functions see Fractalforum^[12]

Dynamic plane for $f_{c}$

Level curves of escape time

Preimages of circle under fc

Julia set by IIM/J

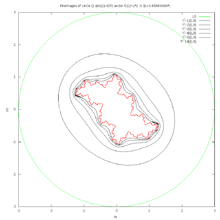
Preimages of repelling fixed point tend to Julia set for C = i. Image and source code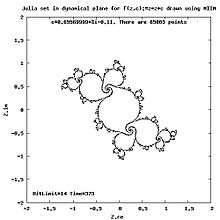
Julia set made with MIIM. Image and maxima source code
Preimages of critical orbit tend to whole Julia set in Siegel disc case
distribution of points in simple IIM/J

In escape time one computes forward iteration of point z.

In IIM/J one computes:

repelling fixed point^[13] of complex quadratic polynomial $Z_{0}=\beta _{c}\,$
preimages of $Z_{0}\,$ by inverse iterations

$Z_{n-1}={\sqrt {Z_{n}-C}}$

Because square root is multivalued function then each $Z_{n}\,$ has two preimages $Z_{n-1}\,$ . Thus inverse iteration creates binary tree.

Root of tree

repelling fixed point^[16] of complex quadratic polynomial $Z_{0}=\beta _{c}\,$
- beta
other repelling periodic points ( cut points of filled Julia set ). It will be important especially in case of the parabolic Julia set.

"... preimages of the repelling fixed point beta. These form a tree like

                                               beta
                    beta                                            -beta
   beta                         -beta                    x                     y

So every point is computed at last twice when you start the tree with beta. If you start with -beta, you will get the same points with half the number of computations.

Something similar applies to the preimages of the critical orbit. If z is in the critical orbit, one of its two preimages will be there as well, so you should draw -z and the tree of its preimages to avoid getting the same points twice." (Wolf Jung )

Variants of IIM

random choose one of two roots IIM ( up to chosen level max). Random walk through the tree. Simplest to code and fast, but inefficient. Start from it.
- both roots with the same probability
- more often one then other root
draw all roots ( up to chosen level max)^[17]
- using recurrence
- using stack ( faster ?)
draw some rare paths in binary tree = MIIM. This is modification of drawing all roots. Stop using some rare paths.
- using hits table ( while hit(pixel(iX,iY)) < HitMax )^[18]
- using derivative ( while derivative(z) < DerivativeMax)^[19]<ref>Drakopoulos V., Comparing rendering methods for Julia sets, Journal of WSCG 10 (2002), 155â161</re>

Examples of code :

Maxima CAS source code - simple IIM . Click on the right to view

It is only one function for all code see here

 
 finverseplus(z,c):=sqrt(z-c);
 finverseminus(z,c):=-sqrt(z-c);
 c:%i;    /*       define c value  */
 iMax:5000;  /* maximal number of reversed iterations */

 fixed:float(rectform(solve([z*z+c=z],[z])));  /* compute fixed points of f(z,c) :   z=f(z,c)   */

 if (abs(2*rhs(fixed[1]))<1)  /* Find which is repelling  */
     then block(beta:rhs(fixed[1]),alfa:rhs(fixed[2])) 
     else block(alfa:rhs(fixed[1]),beta:rhs(fixed[2]));

  z:beta; /* choose repeller as a starting point */

 /* make 2 list of points and copy beta to lists */ 
 xx:makelist (realpart(beta), i, 1, 1); /* list of re(z) */
 yy:makelist (imagpart(beta), i, 1, 1); /* list of im(z) */ 

 for i:1 thru iMax  step 1 do  /* reversed iteration of beta */
 block
 (if random(1.0)>0.5 /* random choose of one of two roots  */
   then z:finverseplus(z,c)
   else z:finverseminus(z,c),
  xx:cons(realpart(z),xx), /* save values to draw it later */
  yy:cons(imagpart(z),yy)
 );


 plot2d([discrete,xx,yy],[style,[points,1,0,1]]); /* draw reversed orbit of beta */

Compare it with:

C code.
Matlab code

Maxima CAS source code - MIIM using hit table . Click on the right to view