Fractals/Iterations in the complex plane/parabolic

< Fractals < Iterations in the complex plane

"Most programs for computing Julia sets work well when the underlying dynamics is hyperbolic but experience an exponential slowdown in the parabolic case." ( Mark Braverman )^[1]

In other words it means that one can need days for making a good picture of parabolic Julia set with standard / naive algorithms.

There are 2 problems here :

slow (= lazy) local dynamics ( in the neighbourhood of a parabolic fixed point )
some parts are very thin ( hard to find using standard plane scanning)

Planes

Dynamic plane

Discrete dynamic in case of complex quadratic polynomial. exterior = white, interior = gray, unknown=red;

How image is changing with various Iteration Max

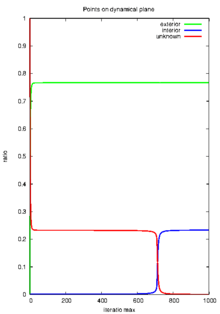
Dynamic plane = complex z-plane $\mathbb {C} =J_{f}\cup F_{f}$ :

Julia set $J_{f}\subset \mathbb {C}$ is a common boundary : $J_{f}\,=\partial A_{f}(p)=\partial A_{f}(\infty )$
Fatou set $F_{f}\subset \mathbb {C}$
- exterior of Julia set = basin of attraction to infinity : $A_{f}(\infty )\ {\overset {\underset {\mathrm {def} }{}}{=}}\ \{z\in \mathbb {C} :f^{(k)}(z)\to \infty \ as\ k\to \infty \}.$
- interior of Julia set = basin of attraction of finite, parabolic fixed point p : $A_{f}(p)\ {\overset {\underset {\mathrm {def} }{}}{=}}\ \{z\in \mathbb {C} :f^{(k)}(z)\to p\ as\ k\to \infty \}.$
  - immediate basin = sum of componets which have parabolic fixed point p on it's boundary ; the immediate parabolic basin of p is the union of periodic connected components of the parabolic basin.
    - attracting Lea-Fatou flower = sum of n attracting petals = sum of 2*n attracting sepals
      - petal = part of the flower. Each petal contains part of 2 sepals,
      - sepals ( Let 1 be an invariant curve in the first quadrant and L 1 the region enclosed by 1 ∪ {0}, called a sepal. ) ^[2]

$\mathbb {C} \supset F(f)\supset A_{f}(p)$

Key words

parabolic chessboard or checkerboard
parabolic implosion
Fatou coordinate
Gevrey symptotic expansions
- the Écalle-Voronin invariants of (7.1) at the origin which have Gevrey- 1/2 asymptotic expansions^[4]
germ^[5]^[6] ^[7]
- germ of the function : Taylor expansion of the function
multiplicity^[8]
Julia-Lavaurs sets
The Leau-Fatou flower theorem^[9] : repelling or attracting flower. Flower consist of petals
Parabolic Linearization theorem
The horn map
Blaschke product
Inou and Shishikura's near parabolic renormalization
complex polynomial vector field ^[10]
numbers
- "a positive integer ν, the parabolic degeneracy with the following property: there are νq attracting petals and νq repelling petals, which alternate cyclically around the fixed point." ^[11]
- combinatorial rotation number
a Poincaré linearizer of function f at parabolic fixed point^[12]

Ecalle cilinder

Ecalle cylinders^[13] or Ecalle-Voronin cylinders ( by Jean Ecalle^[14] ^[15])

"... the quotient of a petal P under the equivalence relation identifying z and f (z) if both z and f (z) belong to P. This quotient manifold is called the Ecalle cilinder, and it is conformally isomorphic to the infinite cylinder C/Z"^[16]

eggbeater dynamics

Hand Egg beater

Here is real model of what happens in parabolic case

It is a dynamic plane for fc(z)=z^2 + 1/4. It is zoom around parabolic fixed point z=0.5. Orbits of some points inside Julia set are shown (white points)

Contunuus model of dynamics inside a 2 petals flower - dipol

Model of dynamics inside a 4 petals flower - quadrupole

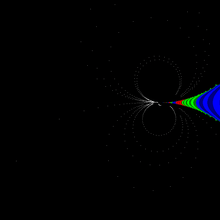
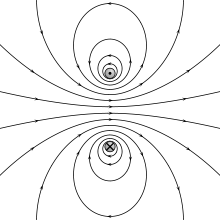
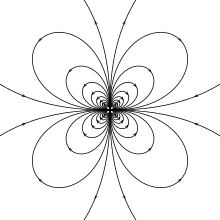
Physical model : the behaviour of cake when one uses eggbeater.

The mathematical model : a 2D vector field with 2 centers ( second-order degenerate points ) ^[17]^[18]

The field is spinning about the centers, but does not appear to be diverging.

parabolic germ

Germ : ^[19]^[20]^[21]

z+z^2
z+z^3
z+z^{k+1}
z+a_{k+1}z^{k+1}
z+a_{k+1}z^{k+1}
"a germ $f(x)=a_{1}x+a_{2}x^{2}+\ldots$ with $\vert a_{1}\vert \neq 0,1$ is holomorphically conjugated to its linear part $g(x)=a_{1}z$ " ( Sylvain Bonnot )^[22]

germ of vector field

The horn map

" the horn map h = Φ ◦ Ψ, where Φ is a shorthand for Φattr and Ψ for Ψrep (extended Fatou coordinate and parameterizations)." ^[23]

Petal

repelling petals around fixed point and its preimages

"The petals ... are interesting not only because they give a rather good intuitive idea of the dynamics that arise near a parabolic point, but also because that the dynamic of f0 on a petal can be linearized, i.e., it is conjugated to the shift map T of C defined by T(w) := w + 1." ( Laurea Triennale ^[24] )

There is no unified definition of petals.

Petal of a flower can be :

attracting / repelling
small/alfa/big/ ( small attracting petals do not ovelap with repelling petals, but big do)

Each petal is invariant under f^period. In other words it is mapped to itself by f^period.

Attracting petal P is a :

Each petal is invariant under $f^{n}$ . In other words it is mapped to itself by $f^{n}$ : $f^{n}({\overline {P}})\subset P\cup \left\{p\right\}$
domain (topological disc ) containing :
- parabolic periodic point p in its boundary ${\overline {P}}\ni \left\{p\right\}$ ( precisely in its root , which is a coomon points of all attracting and repelling petals = center of the Lea-Fatou flower)
- critical point or it's n=period images on the other side ( only small ?? )
trap which captures any orbit tending to parabolic point ^[25]
set contained inside component of filled-in Julia set. The attracting petals of parabolic fixed point are contained in it's basin of attraction
" ... is maximal with respect to this property. This preferred petal P max always has one or more critical points on its boundary."^[26]
"an attracting petal is the interior of an analytic curve which lies entirely in the Fatou set, has the right tangency property at the fixed point, and is mapped into its interior by the correct power of the map" Scott Sutherland

Petals $P_{j}$ are symmetric with respect to the d-1 directions :

$arg(z)={\frac {2\Pi l}{d-1}}$

where :

d is (to do)
l is from 0 to d-2

Petals can have different size.

If $\lambda ^{n}=1$ then Julia set should approach parabolic periodic point in n directions, between n petals. ^[27]

" Using the language of holomorphic dynamics, people would say that you are studying the dynamics of a polynomial near the parabolic fixed point $z=0$ . By a simple linear change of variables, the study of any such parabolic fixed point can be reduced to the study of $z\mapsto z+z^{2}+O(z^{3})$ . Then you can apply another change $w=-{\frac {1}{z}}$ . Thus you are reduced to the study of $f(w)=w+1+O(1/w)$ . If the real part $Re(w)$ is large enough you will obtain $f^{n}(w)=w+n+O(\log n)$ . This will give you what you want (when going back to the z-variable).

The domain $Re(w)>R$ (for large $R$ ) looks like some kind of cardioid (in your particular case) when you visualize it in the z-variable (it's poetically called an attracting petal). " Sylvain Bonnot ^[28]

0/1

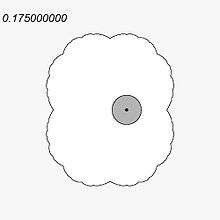
How the target set is changing along an internal ray 0

Cpp code by Wolf Jung see function parabolic from file mndlbrot.cpp ( program mandel ) ^[29]^[30]

To see effect :

run Mandel
(on parameter plane ) find parabolic point for angle 0, which is c=0.25. To do it use key c, in window input 0 and return.

C code :

  // in function uint mndlbrot::esctime(double x, double y)
  if (b == 0.0 && !drawmode && sign < 0
      && (a == 0.25 || a == -0.75)) return parabolic(x, y);
 // uint mndlbrot::parabolic(double x, double y)
 if (Zx>=0 && Zx <= 0.5 && (Zy > 0 ? Zy : -Zy)<= 0.5 - Zx) 
            { if (Zy>0) data[i]=200; // show petal
                     else data[i]=150;}

Gnuplot code :

reset
f(x,y)=  x>=0 && x<=0.5 &&  (y > 0 ? y : -y) <= 0.5 - x
unset colorbox
set isosample 300, 300
set xlabel 'x'
set ylabel 'y'
set sample 300
set pm3d map
splot [-2:2] [-2:2] f(x,y)

1/2

Cpp code by Wolf Jung see function parabolic from file mndlbrot.cpp ( program mandel ) ^[31] To see effect :

run Mandel
(on parameter plane ) find parabolic point for angle 1/2, which is c=-0.75. To do it use key c, in window input 0 and return.

C code :

  // in function uint mndlbrot::esctime(double x, double y)
  if (b == 0.0 && !drawmode && sign < 0
      && (a == 0.25 || a == -0.75)) return parabolic(x, y);
 // uint mndlbrot::parabolic(double x, double y)
  if (A < 0 && x >= -0.5 && x <= 0 && (y > 0 ? y : -y) <= 0.3 + 0.6*x)
      {  if (j & 1) return (y > 0 ? 65282u : 65290u);
         else return (y > 0 ? 65281u : 65289u);
      }

1/3

Method by Scott Sutherland:

choose the connected component containing the critical point
find an analytic curve which lies entirely in the Fatou set, has the right tangency property at the fixed point, and is mapped into its interior by the correct power of the map
the other two are just the image of this curve under the first and second iterates.

Number of petals

In parabolic point child period coincides with parent period

For quadratic polynomials :

Multiplicity = ParentPeriod + ChildPeriod

NumberOfPetals = multiplicity - ParentPeriod

It is because in parabolic case fixed point coincidence with periodic cycle. Length of cycle ( child period) is equal to number of petals

For other polynomial maps :

One critical point and 5 petals
13 critical points and 26 petals.
14 critical points and 14 petals.
z^4-z has 3 critical points and 6 petals

f(z)	number of petals	explanation
$z^{d}+z$	d-1	for $z^{d}+z=z$ point z=0 has multiplicity d
$z^{d}-z$	d+2	(?)for $f^{2}(z)$ a root z=0 has multiplicity d+3

For f(z)= -z+z^(p+1) parabolic flower has :

2p petals for p odd
p petals for p even ^[32]

... ( to do )

Sepal

Sepals and petals

Parabolic sepals for internal angle 1 over 1

Definitions:

A sepal is the intersection of an attracting and repelling petal.A parabolic Pommerenke-Levin-Yoccoz inequality. by Xavier Buf and Adam L. Epstein There does not seem to be an official definition of sepal.
"Let l be an invariant curve in the first quadrant and L1 the region enclosed by l ∪ {0}, called a sepal." ^[33]

Flower

Lea-Fatu flower
Flower with four petals and parabolic point in the center
Critical orbit for internal angle 1/5 showing 5 attracting directions

Sum of all petals creates a flower with center at parabolic periodic point.^[34]

"... an attracting petal is a set of points in a sufficient small disk around the periodic point whose forward orbits always remain in the disk under powers of return map. " ( W P Thurston : On the geometry and dynamics of Iterated rational maps)

Cauliflower

Cauliflower or broccoli :^[35]

empty ( its interior is empty ) for c outside Mandelbrot set. Julia set is a totally disconnected (
filled cauliflower for c=1/4 on boundary of the Mandelbrot set. Julia set is a Jordan curve ( quasi circle).

c = 0 < 1/4
c = 0.25 = 1/4 t he root of the main cardioid. Julia set is a cauliflower
c = 0.255 > 1/4 "imploded cauliflower"
c = 0.258 > 1/4
c = [0.285, 0.01]

Pleae note that :

size of image differs because of different z-planes.
different algorithms are used so colours are hard to compare

Bifurcation of the Cauliflower

How Julia set changes along real axis ( going from c=0 thru c=1/4 and futher ) :

Perturbation of a function $f(z)$ by complex $\epsilon$ :

$g(z)=f(z)+\epsilon$

When one add epsilon > 0 ( move along real axis toward + infinity ) there is a bifurcation of parabolic fixed point :

attracting fixed point ( epsilon<0 )
one parabolic fixed point ( epsilon = 0 )
one parabolic fixed point splits up into two conjugate repelling fixed points ( epsilon > 0 )

"If we slightly perturb with epsilon<0 then the parabolic fixed point splits up into two real fixed points on the real axis (one attracting, one repelling). "

See :

demo 2 page 9 in program Mandel by Wolf Jung

parabolic implosion

Video on YouTube^[36]

Vector field

2D vector field and its

singularity

singularity types :

center type : "In this case, one can find a neighborhood of the singular point where all integral curves are closed, inside one another, and contain the singular point in their interior" ^[37]
non-center type : neighborhood of singularity is made of several curvilinear sectors :^[38]

" A curvilinear sector is defined as the region bounded by a circle C with arbitrary small radius and two streamlines S and S! both converging towards singularity. One then considers the streamlines passing through the open sector g in order to distinguish between three possible types of curvilinear sectors."

Local dynamics

Local dynamics :

in the exterior of Julia set
on the Julia set
near parabolic fixed point ( inside Julia set )

Near parabolic fixed point

Orbits near parabolic fixed point and inside Julia set

Why analyze f^p not f ?

Forward orbit of f near parabolic fixed point is composite. It consist of 2 motions :

around fixed point
toward / away from fixed point

How to compute parabolic c values

Description

Parabolic points of period 1 component of Mandelbrot set (parameter plane)
n	Internal angle (rotation number) t = 1/n	The root point c = parabolic parameter	Two external angles of parameter rays landing on the root point c (1/(2^n+1); 2/(2^n+1)	fixed point $z_{\alpha }$	external angles of dynamic rays landing on fixed point $z_{\alpha }$
1	1/1	0.25	(0/1 ; 1/1)	0.5	(0/1 = 1/1)
2	1/2	-0.75	(1/3; 2/3)	-0.5	(1/3; 2/3)
3	1/3	0.64951905283833*%i-0.125	(1/7; 2/7)	0.43301270189222*%i-0.25	(1/7; 2/7; 3/7)
4	1/4	0.5*%i+0.25	(1/15; 2/15)	0.5*%i	(1/15; 2/15; 4/15; 8/15)
5	1/5	0.32858194507446*%i+0.35676274578121	(1/31; 2/31)	0.47552825814758*%i+0.15450849718747	(1/31; 2/31; 4/31; 8/31; 16/31)
6	1/6	0.21650635094611*%i+0.375	(1/63; 2/63)	0.43301270189222*%i+0.25	(1/63; 2/63; 4/63; 8/63; 16/63; 32/63)
7	1/7	0.14718376318856*%i+0.36737513441845	(1/127; 2/127)	0.39091574123401*%i+0.31174490092937	(1/127; 2/127, 4/127; 8/127; 16/127; 32/127, 64/127)
8	1/8	0.10355339059327*%i+0.35355339059327		0.35355339059327*%i+0.35355339059327
9	1/9	0.075191866590218*%i+0.33961017714276		0.32139380484327*%i+0.38302222155949
10	1/10	0.056128497072448*%i+0.32725424859374		0.29389262614624*%i+0.40450849718747

For internal angle n/p parabolic period p cycle consist of one z-point with multiplicity p^[39] and multiplier = 1.0 . This point z is equal to fixed point $z_{alfa}$

Period 1

One can easily compute boundary point c

$c=c_{x}+c_{y}*i$

of period 1 hyperbolic component ( main cardioid) for given internal angle ( rotation number) t using this cpp code by Wolf Jung^[40]


t *= (2*PI); // from turns to radians
cx = 0.5*cos(t) - 0.25*cos(2*t); 
cy = 0.5*sin(t) - 0.25*sin(2*t);

or this Maxima CAS code :

 
/* conformal map  from circle to cardioid ( boundary
 of period 1 component of Mandelbrot set */
F(w):=w/2-w*w/4;

/* 
circle D={w:abs(w)=1 } where w=l(t,r) 
t is angle in turns ; 1 turn = 360 degree = 2*Pi radians 
r is a radius 
*/
ToCircle(t,r):=r*%e^(%i*t*2*%pi);

GiveC(angle,radius):=
(
 [w],
 /* point of  unit circle   w:l(internalAngle,internalRadius); */
 w:ToCircle(angle,radius),  /* point of circle */
 float(rectform(F(w)))    /* point on boundary of period 1 component of Mandelbrot set */
)$

compile(all)$

/* ---------- global constants & var ---------------------------*/
Numerator :1;
DenominatorMax :10;
InternalRadius:1;

/* --------- main -------------- */
for Denominator:1 thru DenominatorMax step 1 do
(
 InternalAngle: Numerator/Denominator,
 c: GiveC(InternalAngle,InternalRadius),
 display(Denominator),
 display(c),
  /* compute fixed point */
 alfa:float(rectform((1-sqrt(1-4*c))/2)), /* alfa fixed point */
 display(alfa)
 )$

Period 2

// cpp code by W Jung http://www.mndynamics.com


t *= (2*PI);  // from turns to radians
cx = 0.25*cos(t) - 1.0;
cy = 0.25*sin(t);

Periods 1-6

/* 


batch file for Maxima CAS 
computing bifurcation points for period 1-6

 Formulae for cycles in the Mandelbrot set II
Stephenson, John; Ridgway, Douglas T.
Physica A, Volume 190, Issue 1-2, p. 104-116.
*/

kill(all);
remvalue(all);


start:elapsed_run_time ();

/* ------------ functions ----------------------*/

/* exponential for of complex number with angle in turns */
 /* "exponential form prevents allroots from working", code by Robert P. Munafo */ 

GivePoint(Radius,t):=rectform(ev(Radius*%e^(%i*t*2*%pi), numer))$ /* gives point of unit circle for angle t in turns */

GiveCirclePoint(t):=rectform(ev(%e^(%i*t*2*%pi), numer))$ /* gives point of unit circle for angle t in turns Radius = 1 */

/* gives a list of iMax points of unit circle */
GiveCirclePoints(iMax):=block(
 [circle_angles,CirclePoints],
 CirclePoints:[],
 circle_angles:makelist(i/iMax,i,0,iMax),
 for t in circle_angles do CirclePoints:cons(GivePoint(1,t),CirclePoints),
 return(CirclePoints) /* multipliers */
)$

/* http://commons.wikimedia.org/wiki/File:Mandelbrot_set_Components.jpg 
Boundary equation  b_n(c,P)=0 
    defines relations between hyperbolic components and unit circle for given period n ,
    allows computation of exact coordinates of hyperbolic componenets.

b_n(w,c), is boundary polynomial ( implicit function of 2 variables ).

*/

GiveBoundaryEq(P,n):=
block(
 if n=1 then return(c + P^2 - P),
 if n=2 then return(- c + P - 1),
 if n=3 then return(c^3 + 2*c^2 - (P-1)*c + (P-1)^2),
 if n=4 then return( c^6 + 3*c^5 + (P+3)* c^4 + (P+3)* c^3  - (P+2)*(P-1)*c^2 - (P-1)^3),
 if n=5 then return(c^15 + 8*c^14 + 28*c^13 + (P + 60)*c^12 + (7*P + 94)*c^11 + 
  (3*P^2 + 20*P + 116)*c^10 + (11*P^2 + 33*P + 114)*c^9 + (6*P^2 + 40*P + 94)*c^8 + 
  (2*P^3 - 20*P^2 + 37*P + 69)*c^7 + (3*P - 11)*(3*P^2 - 3*P - 4)*c^6 + (P - 1)*(3*P^3 + 20*P^2 - 33*P - 26)*c^5 +
  (3*P^2 + 27*P + 14)*(P - 1)^2*c^4 - (6*P + 5)*(P - 1)^3*c^3 + (P + 2)*(P - 1)^4*c^2 - c*(P - 1)^5  + (P - 1)^6),
if n=6 then return( c^27+
13*c^26+
78*c^25+
(293 - P)*c^24+
(792 - 10*P)*c^23+
(1672 - 41*P)*c^22+
(2892 - 84*P - 4*P^2)*c^21+
(4219 - 60*P - 30*P^2)*c^20+
(5313 + 155*P - 80*P^2)*c^19+
(5892 + 642*P - 57*P^2 + 4*P^3)*c^18+
(5843 + 1347*P + 195*P^2 + 22*P^3)*c^17+
(5258 + 2036*P + 734*P^2 + 22*P^3)*c^16+
(4346 + 2455*P + 1441*P^2 - 112*P^3 + 6*P^4)*c^15 + 
(3310 + 2522*P + 1941*P^2 - 441*P^3 + 20*P^4)*c^14 + 
(2331 + 2272*P + 1881*P^2 - 853*P^3 - 15*P^4)*c^13 + 
(1525 + 1842*P + 1344*P^2 - 1157*P^3 - 124*P^4 - 6*P^5)*c^12 + 
(927 + 1385*P + 570*P^2 - 1143*P^3 - 189*P^4 - 14*P^5)*c^11 + 
(536 + 923*P - 126*P^2 - 774*P^3 - 186*P^4 + 11*P^5)*c^10 + 
(298 + 834*P + 367*P^2 + 45*P^3 - 4*P^4 + 4*P^5)*(1-P)*c^9 + 
(155 + 445*P - 148*P^2 - 109*P^3 + 103*P^4 + 2*P^5)*(1-P)*c^8 + 
2*(38 + 142*P - 37*P^2 - 62*P^3 + 17*P^4)*(1-P)^2*c^7 + 
(35 + 166*P + 18*P^2 - 75*P^3 - 4*P^4)*((1-P)^3)*c^6 + 
(17 + 94*P + 62*P^2 + 2*P^3)*((1-P)^4)*c^5 + 
(7 + 34*P + 8*P^2)*((1-P)^5)*c^4 + 
(3 + 10*P + P^2)*((1-P)^6)*c^3 + 
(1 + P)*((1-P)^7)*c^2 +
-c*((1-P)^8) + (1-P)^9)
)$


/* gives a list of points c on boundaries on all components for give period */
GiveBoundaryPoints(period,Circle_Points):=block(
 [Boundary,P,eq,roots],
  Boundary:[],
 for m in Circle_Points do (/* map from reference plane to parameter plane */
  P:m/2^period,
  eq:GiveBoundaryEq(P,period), /* Boundary equation  b_n(c,P)=0  */
  roots:bfallroots(%i*eq),
  roots:map(rhs,roots),
  for root in roots do Boundary:cons(root,Boundary)),
  return(Boundary)
)$


/* divide llist of roots to 3 sublists = 3  components */
/* ---- boundaries of period 3 components 
period:3$
Boundary3Left:[]$
Boundary3Up:[]$
Boundary3Down:[]$

Radius:1;

 for m in CirclePoints do (
  P:m/2^period,
  eq:GiveBoundaryEq(P,period),
  roots:bfallroots(%i*eq),
  roots:map(rhs,roots),
  for root in roots do 
     (
       if realpart(root)<-1  then Boundary3Left:cons(root,Boundary3Left),
       if (realpart(root)>-1 and imagpart(root)>0.5) 
            then Boundary3Up:cons(root,Boundary3Up),
       if (realpart(root)>-1 and imagpart(root)<0.5) 
            then Boundary3Down:cons(root,Boundary3Down)
               
     )

)$
--------- */


/* gives a list of parabolic points for given : period and internal angle */
GiveParabolicPoints(period,t):=block
(
 [m,ParabolicPoints,P,eq,roots],
 m: GiveCirclePoint(t), /* root of unit circle, Radius=1, angle t=0 */
 ParabolicPoints:[],
 /* map from reference plane to parameter plane */
 P:m/2^period,
 eq:GiveBoundaryEq(P,period), /* Boundary equation  b_n(c,P)=0  */
 roots:bfallroots(%i*eq),
 roots:map(rhs,roots),
 for root in roots do ParabolicPoints:cons(float(root),ParabolicPoints),
 return(ParabolicPoints) 

)$


compile(all)$



/* ------------- constant values ----------------------*/

fpprec:16; 





/* ------------unit circle on a w-plane -----------------------------------------*/
a:GiveParabolicPoints(6,1/3);
a$

How to draw parabolic Julia set

5 methods of drawing
Checking iteration
modified DEM
checking angle
checking if zn is in target set
checking if zn is in triangle target set

All points of interior of filled Julia set tend to one periodic orbit ( or fixed point ). This point is in Julia set and is weakly attracting. ^[41] One can analyse only behevior near parabolic fixed point. It can be done using critical orbits.

There are two cases here : easy and hard.

If the Julia set near parabolic fixed point is like n-th arm star ( not twisted) then one can simply check argument of of zn, relative to the fixed point. See for example z+z^5. This is an easy case.

In the hard case Julia set is twisted around fixed.

Estimation from exterior

Escape time

Description

Long iteration method

Long iteration method ^[42]

Dynamic rays

Parabolic Julia set for internal angle 1 over 15 - made with use of external rays as a aproximation of Julia set near alfa fixed point

One can use periodic dynamic rays landing on parabolic fixed point to find narrow parts of exterior.

Let's check how many backward iterations needs point on periodic ray with external radius = 4 to reach distance 0.003 from parabolic fixed point :

period	Inverse iterations	time
1	340	0m0.021s
2	55 573	0m5.517s
3	8 084 815	13m13.800s
4	1 059 839 105	1724m28.990s

C source code - click on the right to view

a.c:

/*
c console program 
to compile  :
 gcc double_t.c -lm -Wall -march=native

to run :
time ./a.out


period	EscapeTime	time
1	       340	 0m0.021s
2	    55 573   	 0m5.517s
3	 8 084 815	13m13.800s 
4    1 059 839 105    1724m28.990s


period 1
escape time   = 340.000000 
internal angle t  = 1.000000 
period  = 1 
preperiod  = 0 
cx  = 0.250000 
cy  = 0.000000 
alfax  = 0.500000 
alfay  = 0.000000 
real	0m0.021s

===============
escape time   = 55573.000000 
internal angle t  = 0.500000 
period  = 2 
preperiod  = 0 
cx  = -0.750000 
cy  = 0.000000 
alfax  = -0.500000 
alfay  = 0.000000 

real	0m5.517s
===============================
period = 3  c = (-0.125000; 0.649519); alfa  = (-0.250000;0.433013)
ea  = 0.142857;
internal angle t  = 0.333333 
preperiod  = 0 
for period = 3  escape time =    8084815 

real	13m13.800s
=====================================
period = 4  c = (0.250000; 0.500000); alfa  = (0.000000;0.500000)
ea  = 0.066667;
internal angle t  = 0.250000 
preperiod  = 0 
for period = 4  escape time = 1059839105 

real	1724m28.990s

*/



#include <stdio.h>
#include <stdlib.h> // malloc
#include <math.h> // M_PI; needs -lm also 
#include <complex.h>

unsigned int period = 4;// of child component of Mandelbrot set
unsigned int numerator=1 ;
unsigned int denominator;
double t ; // internal angle of point c of parent component of Mandelbrot set in turns 
unsigned long int maxiter = 100000;
unsigned int preperiod = 0; //of external angle under doubling map

 double complex z , c, alfa;
  double ea ;// External Angle 




/* find c in component of Mandelbrot set 
 uses complex type so #include <complex.h> and -lm 
 uses code by Wolf Jung from program Mandel
 see function mndlbrot::bifurcate from mandelbrot.cpp
 http://www.mndynamics.com/indexp.html

  */
double complex GiveC(double InternalAngleInTurns, double InternalRadius, unsigned int period)
{
  //0 <= InternalRay<= 1
  //0 <= InternalAngleInTurns <=1
  // period of parent component of Mandelbrot set  { 1,2 }
  double t = InternalAngleInTurns *2*M_PI; // from turns to radians
  double R2 = InternalRadius * InternalRadius;
  double Cx, Cy; /* C = Cx+Cy*i */
  switch ( period ) {
    case 1: // main cardioid
      Cx = (cos(t)*InternalRadius)/2-(cos(2*t)*R2)/4; 
      Cy = (sin(t)*InternalRadius)/2-(sin(2*t)*R2)/4; 
      break;
   case 2: // only one component 
      Cx = InternalRadius * 0.25*cos(t) - 1.0;
      Cy = InternalRadius * 0.25*sin(t); 
      break;
  // for each period  there are 2^(period-1) roots. 
  default: // safe values
      Cx = 0.0;
      Cy = 0.0; 
    break; }

  return Cx+ Cy*I;
}


/*

http://en.wikipedia.org/wiki/Periodic_points_of_complex_quadratic_mappings
z^2 + c = z
z^2 - z + c = 0
ax^2 +bx + c =0 // ge3neral for  of quadratic equation
so :
a=1
b =-1
c = c
so :

The discriminant is the  d=b^2- 4ac 

d=1-4c = dx+dy*i
r(d)=sqrt(dx^2 + dy^2)
sqrt(d) = sqrt((r+dx)/2)+-sqrt((r-dx)/2)*i = sx +- sy*i

x1=(1+sqrt(d))/2 = beta = (1+sx+sy*i)/2

x2=(1-sqrt(d))/2 = alfa = (1-sx -sy*i)/2

alfa : attracting when c is in main cardioid of Mandelbrot set, then it is in interior of Filled-in Julia set, it means belongs to Fatou set ( strictly to basin of attraction of finite fixed point )
*/
// uses global variables : 
//  ax, ay (output = alfa(c)) 
double complex GiveAlfaFixedPoint(double complex c)
{
  double dx, dy; //The discriminant is the  d=b^2- 4ac = dx+dy*i
  double r; // r(d)=sqrt(dx^2 + dy^2)
  double sx, sy; // s = sqrt(d) = sqrt((r+dx)/2)+-sqrt((r-dx)/2)*i = sx + sy*i
  double ax, ay;
 
 // d=1-4c = dx+dy*i
 dx = 1 - 4*creal(c);
 dy = -4 * cimag(c);
 // r(d)=sqrt(dx^2 + dy^2)
 r = sqrt(dx*dx + dy*dy);
 //sqrt(d) = s =sx +sy*i
 sx = sqrt((r+dx)/2);
 sy = sqrt((r-dx)/2);
 // alfa = ax +ay*i = (1-sqrt(d))/2 = (1-sx + sy*i)/2
 ax = 0.5 - sx/2.0;
 ay =  sy/2.0;
 

return ax+ay*I;
}


double DistanceBetween(double complex z1, double complex z2 )
{double dx,dy;
 
 dx = creal(z1) - creal(z2);
 dy = cimag(z1) - cimag(z2);
 return sqrt(dx*dx+dy*dy);
 
} 



/* 
 principal square  root of complex number 
 http://en.wikipedia.org/wiki/Square_root

 z1= I;
  z2 = root(z1);
  printf("zx  = %f \n", creal(z2));
  printf("zy  = %f \n", cimag(z2));
*/
double complex root(double complex z)
{ 
  double x = creal(z);
  double y = cimag(z);
  double u;
  double v;
  double r = sqrt(x*x + y*y); 
  
  v = sqrt(0.5*(r - x));
  if (y < 0) v = -v; 
  u = sqrt(0.5*(r + x));
 return u + v*I;
}

double complex preimage(double complex z1, double complex z2,  double complex c)
{ 
  double complex zPrev;

  zPrev = root(creal(z1) - creal(c) + ( cimag(z1) - cimag(c))*I);
  // choose one of 2 roots 
  if (creal(zPrev)*creal(z2) + cimag(zPrev)*cimag(z2) > 0) 
        return zPrev ;     //  u+v*i
       else return -zPrev; // -u-v*i
}



// This function only works for periodic or preperiodic angles.
// You must determine the period n and the preperiod k before calling this function.
// based on same function from src code of program Mandel by Wolf Jung
// http://www.mndynamics.com/indexp.html
double  backray(double t, // external angle in turns 
		       int n, //period of ray's angle under doubling map
		       int k, // preperiod
                       int iterMax,
                       double complex c
                          )
{
  double xend ; // re of the endpoint of the ray
  double yend; // im of the endpoint of the ray
  const double R = 4; // very big radius = near infinity
  int j; // number of ray 
  double iter=0.0; // index of backward iteration
  
  
  
  double complex zPrev;
  double u,v; // zPrev = u+v*I
  double complex zNext;
  double distance;





   /* dynamic 1D arrays for coordinates ( x, y) of points with the same R on preperiodic and periodic rays  */
  double *RayXs, *RayYs;
  int iLength = n+k+2; // length of arrays ?? why +2
  //  creates arrays :  RayXs and RayYs  and checks if it was done
  RayXs = malloc( iLength * sizeof(double) );
  RayYs = malloc( iLength * sizeof(double) );
  if (RayXs == NULL || RayYs==NULL)
    {
      fprintf(stderr,"Could not allocate memory");
      getchar(); 
      return 1;
    }
  


 //  starting points on preperiodic and periodic rays 
 //  with angles t, 2t, 4t...  and the same radius R
  for (j = 0; j < n + k; j++)
  { // z= R*exp(2*Pi*t)
    RayXs[j] = R*cos((2*M_PI)*t); 
    RayYs[j] = R*sin((2*M_PI)*t);
    t *= 2; // t = 2*t
    if (t > 1) t--; // t = t modulo 1 
  }
  zNext = RayXs[0] + RayYs[0] *I;

  //printf("RayXs[0]  = %f \n", RayXs[0]);
  //printf("RayYs[0]  = %f \n", RayYs[0]);

  // z[k] is n-periodic. So it can be defined here explicitly as well.
  RayXs[n+k] = RayXs[k]; 
  RayYs[n+k] = RayYs[k];

  //   backward iteration of each point z
  do
    { 
     	
        for (j = 0; j < n+k; j++) // period +preperiod
         { // u+v*i = sqrt(z-c)   backward iteration in fc plane 
		zPrev = root(RayXs[j+1] - creal(c)+(RayYs[j+1] - cimag(c))*I ); // , u, v
                u=creal(zPrev);
                v=cimag(zPrev);
                
		// choose one of 2 roots: u+v*i or -u-v*i
		if (u*RayXs[j] + v*RayYs[j] > 0) 
                        { RayXs[j] = u; RayYs[j] = v; } // u+v*i
			else { RayXs[j] = -u; RayYs[j] = -v; } // -u-v*i
         } // for j ...

          //RayYs[n+k] cannot be constructed as a preimage of RayYs[n+k+1]
          RayXs[n+k] = RayXs[k]; 
          RayYs[n+k] = RayYs[k];
          
          // convert to pixel coordinates 
          //  if z  is in window then draw a line from (I,K) to (u,v) = part of ray 
   
       // printf("for iter = %d cabs(z) = %f \n", iter, cabs(RayXs[0] + RayYs[0]*I));
   iter += 1.0;
  distance = DistanceBetween(RayXs[j]+RayYs[j]*I, alfa);
   printf("distance  = %10.9f ; iter = %10.0f \n", distance, iter); // info  
  }
 while (distance>0.003);// distance < pixel size 
 
 // last point of a ray 0
 xend = RayXs[0];
 yend = RayYs[0];

 // free memmory
 free(RayXs);
 free(RayYs);

return  iter; //  
}




/* ---------------------- main ------------------*/
int main()
{
 
 double EscapeTime;
  
  // internal angle
  denominator = period;
  t = (double) numerator/denominator; 
  


  // 
  c = GiveC(t, 1.0, 1);
  alfa = GiveAlfaFixedPoint(c);

  //external angle 
  denominator= pow(2,period) - 1;
  ea = (double) 1.0/ denominator;
  //
  EscapeTime = backray(ea, period, preperiod, maxiter, c );
  
  
  // 
  printf("period = %d ", period );
  printf(" c = (%f; %f);", creal(c), cimag(c));
  printf(" alfa  = (%f;%f)\n", creal(alfa), cimag(alfa));
  printf("ea  = %f;\n", ea);
  printf("internal angle t  = %f \n", t);
  printf("preperiod  = %d \n", preperiod);
  printf("for period = %d  escape time = %10.0f \n", period,  EscapeTime);
  //
  
 
  return 0;
}

One can use only argument of point z of external rays and its distance to alfa fixed point. ( see code from image) It works for periods up to 15 ( maybe more ... )

Estimation from interior

Julia set is a boundary of filled-in Julia set Kc.

find points of interior of Kc
find boundary of interior of Kc using edge detection

If components of interior are lying very close to each other then find components using :^[43]

color = LastIteration % period

For parabolic components between parent and child component :^[44]

periodOfChild = denominator*periodOfParent  
color = iLastIteration % periodOfChild

where denominator is a denominator of internal angle of parent comonent of Mandelbrot set.

Angle

"if the iterate zn of tends to a fixed parabolic point, then the initial seed z0 is classified according to the argument of zn−z0, the classification being provided by the flower theorem " ( Mark McClure ^[45])

Attraction time

Various types of dynamics

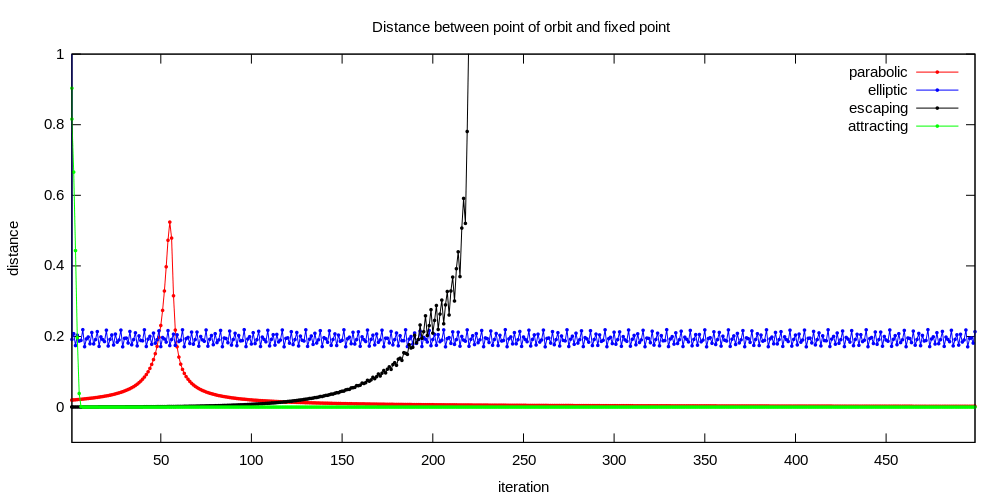
Interior of filled Julia set consist of components. All comonents are preperiodic, some of them are periodic ( immediate basin of attraction).

In other words :

one iteration moves z to another component ( and whole component to another component)
all point of components have the same attraction time ( number of iteration needed to reach target set around attractor)

It is possible to use it to color components. Because in parabolic case attractor is weak ( weakly attracting) it needs a lot of iterations for some points to reach it.

 // i = number of iteration
 // iPeriodChild = period of child component of Mandelbrot set ( parabolic c value is a root point between parant and child component
 /* distance from z to Alpha  */
 Zxt=Zx-dAlfaX;
 Zyt=Zy-dAlfaY;
 d2=Zxt*Zxt +Zyt*Zyt;
 // interior : check if fall into internal target set ( circle around alfa fixed point )  
 if (d2<dMaxDistance2Alfa2) return  iColorsOfInterior[i % iPeriodChild];

Here are some example values :

 iWidth  = 1001 // width of image in pixels
 PixelWidth  = 0.003996  
 AR  = 0.003996 // Radius around attractor
 denominator  = 1 ; Cx  = 0.250000000000000; Cy  = 0.000000000000000 ax  = 0.500000000000000; ay  = 0.000000000000000   
 denominator  = 2 ; Cx  = -0.750000000000000; Cy  = 0.000000000000000 ax  = -0.500000000000000; ay  = 0.000000000000000   
 denominator  = 3 ; Cx  = -0.125000000000000; Cy  = 0.649519052838329 ax  = -0.250000000000000; ay  = 0.433012701892219  
 denominator  = 4 ; Cx  = 0.250000000000000; Cy  = 0.500000000000000 ax  = 0.000000000000000; ay  = 0.500000000000000   
 denominator  = 5 ; Cx  = 0.356762745781211; Cy  = 0.328581945074458 ax  = 0.154508497187474; ay  = 0.475528258147577   
 denominator  = 6 ; Cx  = 0.375000000000000; Cy  = 0.216506350946110 ax  = 0.250000000000000; ay  = 0.433012701892219    
 
 denominator  = 1 ;   i =               243.000000 
 denominator  = 2 ;   i =            31 171.000000 
 denominator  = 3 ;   i =         3 400 099.000000 
 denominator  = 4 ;   i =       333 293 206.000000 
 denominator  = 5 ;   i =    29 519 565 177.000000 
 denominator  = 6 ;   i = 2 384 557 783 634.000000

where :

C = Cx + Cy*i 
a = ax + ay*i // fixed point alpha
i // number of iterations after which critical point z=0.0 reaches disc around fixed point alpha with radius AR
denominator of internal angle ( in turns )
internal angle =  1/denominator

Note that attraction time i is proportional to denominator.

Attraction time for various denominators

Now you see what means weakly attracting.

One can :

use brutal force method ( Attracting radius < pixelSize; iteration Max big enough to let all points from interior reach target set; long time or fast computer )
find better method (:-)) if time is to long for you

Interior distance estimation

Trap

Trap = target set

Estimation from interior and exterior

Julia set is a common boundary of filled-in Julia set and basin of attraction of infinity.

find points of interior/components of Kc
find escaping points
find boundary points using Sobel filter

It works for denominator up to 4.

Inverse iteration of repelling points

Inverse iteration of alfa fixed point. It works good only for cuting point ( where external rays land). Other points still are not hitten.

Bof61

Gallery

Critical orbits in case of one critical point
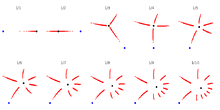critical orbits for internal angle from 1/1 to 1/10. True attracting directions
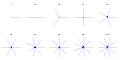N-th arm stars for n from 1 to 10. Schematic attracting directions
critical orbit, attracting and repelling vectors for internal angle 1/3

from period 1 thru ...
1/1 cauliflower
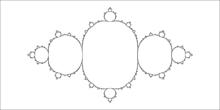1/2 San Marco fractal ^[46]
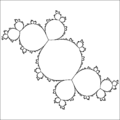1/3 Douady fat rabbit ^[47]
1/4
1/5
1/7
1/10
1/15
1/20
1/30

from period 2 thru ...
from 2 thru internal ray 1/1 ; c=-0.75 Julia set is a San Marco fractal ^[48]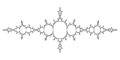
from period 2 thru 1/2
from period 2 thru 1/3
from period 2 thru 1/4

from period 3 thru ...
from period 3 thru 1/3

For other polynomial maps see here

References

This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.