Fractals/Iterations in the complex plane/p misiurewicz

< Fractals < Iterations in the complex plane

How to compute external angles of principal Misiurewicz points^[1] of wakes

names

a principal Misiurewicz points^[2] of wake
the main node of the shrub ^[3]
the hub

introduction

If length of string s is q then

   $\sigma ^{q}s=s$

shifting q digits in blocks of b digits

Note that

   $b<q$

$q=5\ {\text{and}}\ b=1$

  $\sigma ^{0}(s)=\sigma ^{0}(00001)={\color {Red}00001}$ 
  $\sigma ^{1}(s)=\sigma ^{1}(00001)=00010$ 
  $\sigma ^{2}(s)=\sigma ^{2}(00001)=00100$ 
  $\sigma ^{3}(s)=\sigma ^{3}(00001)=01000$ 
  $\sigma ^{4}(s)=\sigma ^{4}(00001)=10000$ 
  $\sigma ^{5}(s)=\sigma ^{5}(00001)={\color {Red}00001}$

$q=5\ {\text{and}}\ b=2$

  $\sigma ^{0}(s)=\sigma ^{0}(00001)={\color {Red}00001}$ 
  $\sigma ^{2}(s)=\sigma ^{2}(00001)=00100$ 
  $\sigma ^{4}(s)=\sigma ^{4}(00001)=10000$

$q=5\ {\text{and}}\ b=3$

  $\sigma ^{0}(s)=\sigma ^{0}(00001)={\color {Red}00001}$ 
  $\sigma ^{3}(s)=\sigma ^{3}(00001)=01000$

$q=5\ {\text{and}}\ b=4$

  $\sigma ^{0}(s)=\sigma ^{0}(00001)={\color {Red}00001}$ 
  $\sigma ^{4}(s)=\sigma ^{4}(00001)=10000$

Algorithm

Algorithm is based on the Theorem 5.3 in: Geometry of the Antennas in the Mandelbrot Set by R L Devaney and M Moreno-Rocha, April 11, 2000^[4]

External Angles of Hub ( see section 3.9 of the Book by Claude) or spoke ^[5]

The $p/q$ bulb ( = hyperbolic component) has 2 external angles landing on it's root point (bond) :

 $\theta _{\color {blue}-}(p/q)=0.({\color {blue}s_{-}})$  
 $\theta _{\color {red}+}(p/q)=0.({\color {red}s_{+}})$

such that :

  $\theta _{\color {blue}-}<\theta _{\color {red}+}$

These angles have :

repeating binary expansion denoted by round brackets or overline
length of repeating ( periodic ) part is $q$

Other names of these angles are angles of the wake.

The junction point of its hub ( principal Misiurewicz point) $M$ has external angles in increasing order

  $0.s_{-}(s_{+})$  
  $0.s_{-}(\sigma ^{b}s_{+})$  
  $\vdots$ 
  $.s_{-}(\sigma ^{(q-p-1)b}s_{+})$ 
  $.s_{+}(\sigma ^{(q-p)b}s_{+})$ 
  $\vdots$ 
  $0.s_{+}(s_{-})$

where

s is a finite string of q binary digits = s consist of q binary digits = length(s)= q
$\sigma$ is the shift map
${\frac {p}{q}}$ fraction has Farey parents :

${\begin{cases}{\frac {a}{b}}<{\frac {p}{q}}<{\frac {r}{s}}\\{\frac {a}{b}}\oplus {\frac {r}{s}}={\frac {p}{q}}\\\end{cases}}$

input and output

input : 2 external angles of the wake $p/q$
output : $q$ external angles of principal Misiurewicz point ( hub)

steps

input = $p/q$
- check input
- if input is good then there are $q$ angles to compute
compute 2 angles of the wake : $s_{-}(p/q)$ and $s_{+}(p/q)$
compute first 2 of q angles : $0.s_{-}(s_{+})$ and $0.s_{+}(s_{-})$
compute last $q-2$ angles
- compute Farey parents of $p/q$
- compute $q-p$
- ( to do )

Examples

1/3

The ${\frac {p}{q}}={\frac {1}{3}}$ bulb ( = period 3 hyperbolic component) has 2 external angles landing on it's root point (bond) :

  $\theta _{-}(1/3)=0.({\color {Blue}s_{-}})=0.({\color {Blue}001})$ 
  $\theta _{+}(1/3)=0.({\color {Red}s_{+}})=0.({\color {Red}010})$

such that :

  $\theta _{-}<\theta _{+}$

Principal Misiurewicz point $M$ of ${\frac {1}{3}}$ wake is a landing point for $q=3$ external angles. It is denoted by

  $c=M_{3,1}=$

where :

first number denotes preperiod
second number denotes period

Two of them one can easly compute from angles the wake :

  $\theta _{-}(M)=0.{\color {Blue}s_{-}}({\color {Red}s_{+}})=0.{\color {Blue}001}({\color {Red}010})$ 
  $\theta _{+}(M)=0.{\color {Red}s_{+}}({\color {Blue}s_{-}})=0.{\color {Red}010}({\color {Blue}001})$

such that :

  ${\color {Blue}s_{-}}<{\color {Blue}s_{-}}({\color {Red}s_{+}})<{\color {Red}s_{+}}({\color {Blue}s_{-}})<{\color {Red}s_{+}}$

So the problem is to compute only 1 ray.

First find Farey parents^[6] of ${\frac {1}{3}}$

Farey diagram

  ${\frac {0}{1}}\oplus {\frac {1}{2}}={\frac {0+1}{1+2}}={\frac {1}{3}}$

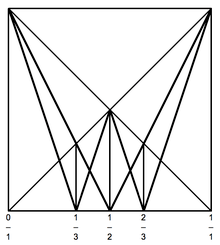
such that :

   ${\frac {0}{1}}<{\frac {1}{3}}<{\frac {1}{2}}$

Take denominator of lower parent :

  $b=1$

and compute last fraction.

First find periodic part :

remember that shift map works on the infinite sequence
take only first q digits from result of shift map

  $\sigma ^{b}({\color {Red}s_{+}})=\sigma (\color {Red}010\ 010\ 010\color {Black}...)=\color {Green}100$

then last angle is :

   $0.{\color {Blue}s_{-}}({\color {Green}\sigma ^{b}s_{+}})=0.{\color {Blue}001}({\color {Green}100})$

So here are 5 angles (q+2) in increasing order :

   ${\begin{aligned}&\theta _{-}(1/3)&=&\ 0.({\color {Blue}s_{-}})&=&0.({\color {Blue}001})&&{\text{ lower angle of the wake}}\\&\theta _{-}(M)&=&\ 0.\ {\color {Blue}s_{-}}({\color {Red}s_{+}})&=&0.\ {\color {Blue}001}\ ({\color {Red}010})&&{\text{ lower angle of M}}\\&\theta _{m}(M)&=&\ 0.\ {\color {Blue}s_{-}}({\color {Green}\sigma s_{+}})&=&0.\ {\color {Blue}001}\ ({\color {Green}100})&&{\text{ middle angle of M}}\\&\theta _{+}(M)&=&\ 0.\ {\color {Red}s_{+}}({\color {Blue}s_{-}})&=&0.\ {\color {Red}010}\ ({\color {Blue}001})&&{\text{ upper angle of M}}\\&\theta _{+}(1/3)&=&\ 0.({\color {Red}s_{+}})&=&0.({\color {Red}010})&&{\text{upper angle of the wake}}\\\end{aligned}}$

1/4

The ${\frac {p}{q}}={\frac {1}{4}}$ bulb ( = period 4 hyperbolic component) has 2 external angles landing on it's root point (bond) :

  $\theta _{-}(1/4)=0.(s_{-})=0.({\color {Blue}0001})$ 
  $\theta _{+}(1/4)=0.(s_{+})=0.({\color {Red}0010})$

Principal Misiurewicz point $M$ of ${\frac {1}{4}}$ wake is a landing point for $q=4$ external angles.

Two of them one can easly compute from angles the wake :

  $\theta _{-}(M)=0.s_{-}(s_{+})=0.{\color {Blue}0001}({\color {Red}0010})$ 
  $\theta _{+}(M)=0.s_{+}(s_{-})=0.{\color {Red}0010}({\color {Blue}0001})$

So the problem is to compute only $q-2=2$ rays.

First find Farey parents of ${\frac {1}{4}}$

Farey diagram

  ${\frac {0}{1}}\oplus {\frac {1}{3}}={\frac {0+1}{1+3}}={\frac {1}{4}}$

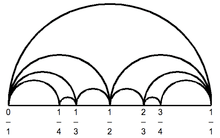
Take denominator of lower parent :

  $b=1$

and compute last fractions.

First find periodic parts for n :

 $\sigma ^{1}(s_{+})=\sigma ^{1}({\color {Red}0010\ 0010\ 0010}...)=\color {Green}0100$ 
 $\sigma ^{2}(s_{+})=\sigma ^{2}({\color {Red}0010\ 0010\ 0010}...)=\color {Magenta}1000$

then 2 last angles are :

   $0.s_{-}(\sigma ^{1}s_{+})=0.{\color {Blue}0001}({\color {Green}0100})$ 
   $0.s_{-}(\sigma ^{2}s_{+})=0.{\color {Red}0010}({\color {Magenta}1000})$

So here are $q+2=6$ angles in increasing order :

   ${\begin{aligned}&\theta _{-}(1/4)&=&0.(s_{-})&=&0.({\color {Blue}0001})&&{\text{ lower angle of the wake}}\\&\theta _{-}(M)&=&0.s_{-}\ (\quad s_{+})&=&0.\ {\color {Blue}0001}\ ({\color {Red}0010})&&{\text{ lower angle of M}}\\&\theta _{m-}(M)&=&\ 0.s_{-}(\sigma ^{1}s_{+})&=&0.\ {\color {Blue}0001}\ ({\color {Green}0100})&&{\text{ middle angle of M}}\\&\theta _{m+}(M)&=&\ 0.s_{-}(\sigma ^{2}s_{+})&=&0.\ {\color {Blue}0001}\ ({\color {Magenta}1000})&&{\text{ middle angle of M}}\\&\theta _{+}(M)&=&0.s_{+}\ (\quad s_{-})&=&0.\ {\color {Red}0010}\ ({\color {Blue}0001})&&{\text{ upper angle of M}}\\&\theta _{+}(1/4)&=&0.(s_{+})&=&0.({\color {Red}0010})&&{\text{upper angle of the wake}}\\\end{aligned}}$

Code

Haskell code

-- Haskell code by Claude Heiland-Allen
-- http://mathr.co.uk/blog/

import Control.Monad (forM_)
import Data.List (genericTake, genericDrop, intercalate)
import Data.Fixed (mod')
import Data.Ratio ((%), numerator, denominator)
import Numeric (readInt)
import System.Environment (getArgs)

type InternalAngle = Rational

type ExternalAngle = ([Bool], [Bool])

pretty :: ExternalAngle -> String
pretty (pre, per) = bits pre ++ "p" ++ bits per

bits :: [Bool] -> String
bits = map bit

bit :: Bool -> Char
bit False = '0'
bit True = '1'

binary :: [Bool] -> Integer
binary [] = 0
binary s = case readInt 2 (`elem`"01") (\c -> case c of '0' -> 0 ; '1' -> 1) (bits s) of
  [(b, "")] -> b

rational :: ExternalAngle -> Rational
rational (pre, per) = (binary pre % 2^p) + (binary per % (2^p * (2^q - 1)))
  where
    p = length pre
    q = length per

bulb :: InternalAngle -> (ExternalAngle, ExternalAngle)
bulb pq = (([], bs ++ [False, True]), ([], bs ++ [True, False]))
  where
    q = denominator pq
    bs
      = genericTake (q - 2)
      . map (\x -> 1 - pq < x && x < 1)
      . iterate (\x -> (x + pq) `mod'` 1)
      $ pq

hub :: InternalAngle -> [ExternalAngle]
hub pq =
  [ (sm, shift k sp) | k <- [0, b .. (q - p - 1) * b] ] ++
  [ (sp, shift k sp) | k <- [(q - p) * b, (q - p + 1) * b .. (q - 1) * b] ]
  where
    p = numerator pq
    q = denominator pq
    (([], sm), ([], sp)) = bulb pq
    (ab, cd) = parents pq
    b = denominator ab
    shift k = genericTake q . genericDrop k . cycle

parents :: InternalAngle -> (InternalAngle, InternalAngle)
parents pq = go q 1 0 p 0 1
  where
    p = numerator pq
    q = denominator pq
    go r1 s1 t1 r0 s0 t0
      | r0 == 0 =
          let ab = - s1 % t1
              a = numerator ab
              b = denominator ab
              c = p - a
              d = q - b
              cd = c % d
          in  (min ab cd, max ab cd)
      | otherwise =
          let (o, r) = divMod r1 r0
              s = s1 - o * s0
              t = t1 - o * t0
          in  go r0 s0 t0 r s t

main :: IO ()
main = do
  [sp, sq] <- getArgs
  p <- readIO sp
  q <- readIO sq
  let pq = p % q
      (lo, hi) = bulb pq
      hs = hub pq
  putStrLn $ "bulb:"
  putStrLn $ pretty lo ++ " = " ++ show (rational lo)
  putStrLn $ pretty hi ++ " = " ++ show (rational hi)
  putStrLn $ ""
  putStrLn $ "hub:"
  forM_ hs $ \h -> putStrLn $ pretty h ++ " = " ++ show (rational h)

Save it as a bh.hs and use it from console in an interactive way :

ghci
GHCi, version 7.10.3: http://www.haskell.org/ghc/  :? for help
Prelude> :l bh.hs
[1 of 1] Compiling Main             ( bh.hs, interpreted )
Ok, modules loaded: Main.

*Main> :main 1 2
bulb:
p01 = 1 % 3
p10 = 2 % 3

hub:
01p10 = 5 % 12
10p01 = 7 % 12
 

*Main> :main 1 3
bulb:
p001 = 1 % 7
p010 = 2 % 7

hub:
001p010 = 9 % 56
001p100 = 11 % 56
010p001 = 15 % 56

*Main> :main 1 4
bulb:
p0001 = 1 % 15
p0010 = 2 % 15

hub:
0001p0010 = 17 % 240
0001p0100 = 19 % 240
0001p1000 = 23 % 240
0010p0001 = 31 % 240

:main 1 5
bulb:
p00001 = 1 % 31
p00010 = 2 % 31

hub:
00001p00010 = 33 % 992
00001p00100 = 35 % 992
00001p01000 = 39 % 992
00001p10000 = 47 % 992
00010p00001 = 63 % 992



*Main> :main 1 6
bulb:
p000001 = 1 % 63
p000010 = 2 % 63

hub:
000001p000010 = 65 % 4032
000001p000100 = 67 % 4032
000001p001000 = 71 % 4032
000001p010000 = 79 % 4032
000001p100000 = 95 % 4032
000010p000001 = 127 % 4032

*Main> :main 1 7
bulb:
p0000001 = 1 % 127
p0000010 = 2 % 127

hub:
0000001p0000010 = 129 % 16256
0000001p0000100 = 131 % 16256
0000001p0001000 = 135 % 16256
0000001p0010000 = 143 % 16256
0000001p0100000 = 159 % 16256
0000001p1000000 = 191 % 16256
0000010p0000001 = 255 % 16256



*Main> :main 1 8
bulb:
p00000001 = 1 % 255
p00000010 = 2 % 255

hub:
00000001p00000010 = 257 % 65280
00000001p00000100 = 259 % 65280
00000001p00001000 = 263 % 65280
00000001p00010000 = 271 % 65280
00000001p00100000 = 287 % 65280
00000001p01000000 = 319 % 65280
00000001p10000000 = 383 % 65280
00000010p00000001 = 511 % 65280


*Main> :main 1 9
bulb:
p000000001 = 1 % 511
p000000010 = 2 % 511

hub:
000000001p000000010 = 513 % 261632
000000001p000000100 = 515 % 261632
000000001p000001000 = 519 % 261632
000000001p000010000 = 527 % 261632
000000001p000100000 = 543 % 261632
000000001p001000000 = 575 % 261632
000000001p010000000 = 639 % 261632
000000001p100000000 = 767 % 261632
000000010p000000001 = 1023 % 261632


*Main> :main 1 10
bulb:
p0000000001 = 1 % 1023
p0000000010 = 2 % 1023

hub:
0000000001p0000000010 = 1025 % 1047552
0000000001p0000000100 = 1027 % 1047552
0000000001p0000001000 = 1031 % 1047552
0000000001p0000010000 = 1039 % 1047552
0000000001p0000100000 = 1055 % 1047552
0000000001p0001000000 = 1087 % 1047552
0000000001p0010000000 = 1151 % 1047552
0000000001p0100000000 = 1279 % 1047552
0000000001p1000000000 = 1535 % 1047552
0000000010p0000000001 = 2047 % 1047552

*Main> :main 1 5
bulb:
p00001 = 1 % 31
p00010 = 2 % 31

hub:
00001p00010 = 33 % 992
00001p00100 = 35 % 992
00001p01000 = 39 % 992
00001p10000 = 47 % 992
00010p00001 = 63 % 992
*Main> :main 2 5
bulb:
p01001 = 9 % 31
p01010 = 10 % 31

hub:
01001p01010 = 289 % 992
01001p10010 = 297 % 992
01001p10100 = 299 % 992
01010p00101 = 315 % 992
01010p01001 = 319 % 992
*Main> :main 3 5
bulb:
p10101 = 21 % 31
p10110 = 22 % 31

hub:
10101p10110 = 673 % 992
10101p11010 = 677 % 992
10110p01011 = 693 % 992
10110p01101 = 695 % 992
10110p10101 = 703 % 992
*Main>  :main 4 5
bulb:
p11101 = 29 % 31
p11110 = 30 % 31

hub:
11101p11110 = 929 % 992
11110p01111 = 945 % 992
11110p10111 = 953 % 992
11110p11011 = 957 % 992
11110p11101 = 959 % 992
*Main> 


*Main> :main 1  7
bulb:
p0000001 = 1 % 127
p0000010 = 2 % 127

hub:
0000001p0000010 = 129 % 16256
0000001p0000100 = 131 % 16256
0000001p0001000 = 135 % 16256
0000001p0010000 = 143 % 16256
0000001p0100000 = 159 % 16256
0000001p1000000 = 191 % 16256
0000010p0000001 = 255 % 16256


*Main> :main 2  7
bulb:
p0010001 = 17 % 127
p0010010 = 18 % 127

hub:
0010001p0010010 = 2177 % 16256
0010001p0100010 = 2193 % 16256
0010001p0100100 = 2195 % 16256
0010001p1000100 = 2227 % 16256
0010001p1001000 = 2231 % 16256
0010010p0001001 = 2295 % 16256
0010010p0010001 = 2303 % 16256



*Main> :main 3 7
bulb:
p0101001 = 41 % 127
p0101010 = 42 % 127

hub:
0101001p0101010 = 5249 % 16256
0101001p1001010 = 5281 % 16256
0101001p1010010 = 5289 % 16256
0101001p1010100 = 5291 % 16256
0101010p0010101 = 5355 % 16256
0101010p0100101 = 5371 % 16256
0101010p0101001 = 5375 % 16256



*Main> :main 4  7
bulb:
p1010101 = 85 % 127
p1010110 = 86 % 127

hub:
1010101p1010110 = 10881 % 16256
1010101p1011010 = 10885 % 16256
1010101p1101010 = 10901 % 16256
1010110p0101011 = 10965 % 16256
1010110p0101101 = 10967 % 16256
1010110p0110101 = 10975 % 16256
1010110p1010101 = 11007 % 16256





*Main> :main 5  7
bulb:
p1101101 = 109 % 127
p1101110 = 110 % 127

hub:
1101101p1101110 = 13953 % 16256
1101101p1110110 = 13961 % 16256
1101110p0110111 = 14025 % 16256
1101110p0111011 = 14029 % 16256
1101110p1011011 = 14061 % 16256
1101110p1011101 = 14063 % 16256
1101110p1101101 = 14079 % 16256


*Main> :main 6  7
bulb:
p1111101 = 125 % 127
p1111110 = 126 % 127

hub:
1111101p1111110 = 16001 % 16256
1111110p0111111 = 16065 % 16256
1111110p1011111 = 16097 % 16256
1111110p1101111 = 16113 % 16256
1111110p1110111 = 16121 % 16256
1111110p1111011 = 16125 % 16256
1111110p1111101 = 16127 % 16256
*Main> 



 :main 1 65
bulb:
p00000000000000000000000000000000000000000000000000000000000000001 = 1 % 36893488147419103231
p00000000000000000000000000000000000000000000000000000000000000010 = 2 % 36893488147419103231

hub:
00000000000000000000000000000000000000000000000000000000000000001p00000000000000000000000000000000000000000000000000000000000000010 = 36893488147419103233 % 1361129467683753853816604941579653742592
00000000000000000000000000000000000000000000000000000000000000001p00000000000000000000000000000000000000000000000000000000000000100 = 36893488147419103235 % 1361129467683753853816604941579653742592
00000000000000000000000000000000000000000000000000000000000000001p00000000000000000000000000000000000000000000000000000000000001000 = 36893488147419103239 % 1361129467683753853816604941579653742592
00000000000000000000000000000000000000000000000000000000000000001p00000000000000000000000000000000000000000000000000000000000010000 = 36893488147419103247 % 1361129467683753853816604941579653742592
00000000000000000000000000000000000000000000000000000000000000001p00000000000000000000000000000000000000000000000000000000000100000 = 36893488147419103263 % 1361129467683753853816604941579653742592
00000000000000000000000000000000000000000000000000000000000000001p00000000000000000000000000000000000000000000000000000000001000000 = 36893488147419103295 % 1361129467683753853816604941579653742592
00000000000000000000000000000000000000000000000000000000000000001p00000000000000000000000000000000000000000000000000000000010000000 = 36893488147419103359 % 1361129467683753853816604941579653742592
00000000000000000000000000000000000000000000000000000000000000001p00000000000000000000000000000000000000000000000000000000100000000 = 36893488147419103487 % 1361129467683753853816604941579653742592
00000000000000000000000000000000000000000000000000000000000000001p00000000000000000000000000000000000000000000000000000001000000000 = 36893488147419103743 % 1361129467683753853816604941579653742592
00000000000000000000000000000000000000000000000000000000000000001p00000000000000000000000000000000000000000000000000000010000000000 = 36893488147419104255 % 1361129467683753853816604941579653742592
00000000000000000000000000000000000000000000000000000000000000001p00000000000000000000000000000000000000000000000000000100000000000 = 36893488147419105279 % 1361129467683753853816604941579653742592
00000000000000000000000000000000000000000000000000000000000000001p00000000000000000000000000000000000000000000000000001000000000000 = 36893488147419107327 % 1361129467683753853816604941579653742592
00000000000000000000000000000000000000000000000000000000000000001p00000000000000000000000000000000000000000000000000010000000000000 = 36893488147419111423 % 1361129467683753853816604941579653742592
00000000000000000000000000000000000000000000000000000000000000001p00000000000000000000000000000000000000000000000000100000000000000 = 36893488147419119615 % 1361129467683753853816604941579653742592
00000000000000000000000000000000000000000000000000000000000000001p00000000000000000000000000000000000000000000000001000000000000000 = 36893488147419135999 % 1361129467683753853816604941579653742592
00000000000000000000000000000000000000000000000000000000000000001p00000000000000000000000000000000000000000000000010000000000000000 = 36893488147419168767 % 1361129467683753853816604941579653742592
00000000000000000000000000000000000000000000000000000000000000001p00000000000000000000000000000000000000000000000100000000000000000 = 36893488147419234303 % 1361129467683753853816604941579653742592
00000000000000000000000000000000000000000000000000000000000000001p00000000000000000000000000000000000000000000001000000000000000000 = 36893488147419365375 % 1361129467683753853816604941579653742592
00000000000000000000000000000000000000000000000000000000000000001p00000000000000000000000000000000000000000000010000000000000000000 = 36893488147419627519 % 1361129467683753853816604941579653742592
00000000000000000000000000000000000000000000000000000000000000001p00000000000000000000000000000000000000000000100000000000000000000 = 36893488147420151807 % 1361129467683753853816604941579653742592
00000000000000000000000000000000000000000000000000000000000000001p00000000000000000000000000000000000000000001000000000000000000000 = 36893488147421200383 % 1361129467683753853816604941579653742592
00000000000000000000000000000000000000000000000000000000000000001p00000000000000000000000000000000000000000010000000000000000000000 = 36893488147423297535 % 1361129467683753853816604941579653742592
00000000000000000000000000000000000000000000000000000000000000001p00000000000000000000000000000000000000000100000000000000000000000 = 36893488147427491839 % 1361129467683753853816604941579653742592
00000000000000000000000000000000000000000000000000000000000000001p00000000000000000000000000000000000000001000000000000000000000000 = 36893488147435880447 % 1361129467683753853816604941579653742592
00000000000000000000000000000000000000000000000000000000000000001p00000000000000000000000000000000000000010000000000000000000000000 = 36893488147452657663 % 1361129467683753853816604941579653742592
00000000000000000000000000000000000000000000000000000000000000001p00000000000000000000000000000000000000100000000000000000000000000 = 36893488147486212095 % 1361129467683753853816604941579653742592
00000000000000000000000000000000000000000000000000000000000000001p00000000000000000000000000000000000001000000000000000000000000000 = 36893488147553320959 % 1361129467683753853816604941579653742592
00000000000000000000000000000000000000000000000000000000000000001p00000000000000000000000000000000000010000000000000000000000000000 = 36893488147687538687 % 1361129467683753853816604941579653742592
00000000000000000000000000000000000000000000000000000000000000001p00000000000000000000000000000000000100000000000000000000000000000 = 36893488147955974143 % 1361129467683753853816604941579653742592
00000000000000000000000000000000000000000000000000000000000000001p00000000000000000000000000000000001000000000000000000000000000000 = 36893488148492845055 % 1361129467683753853816604941579653742592
00000000000000000000000000000000000000000000000000000000000000001p00000000000000000000000000000000010000000000000000000000000000000 = 36893488149566586879 % 1361129467683753853816604941579653742592
00000000000000000000000000000000000000000000000000000000000000001p00000000000000000000000000000000100000000000000000000000000000000 = 36893488151714070527 % 1361129467683753853816604941579653742592
00000000000000000000000000000000000000000000000000000000000000001p00000000000000000000000000000001000000000000000000000000000000000 = 36893488156009037823 % 1361129467683753853816604941579653742592
00000000000000000000000000000000000000000000000000000000000000001p00000000000000000000000000000010000000000000000000000000000000000 = 36893488164598972415 % 1361129467683753853816604941579653742592
00000000000000000000000000000000000000000000000000000000000000001p00000000000000000000000000000100000000000000000000000000000000000 = 36893488181778841599 % 1361129467683753853816604941579653742592
00000000000000000000000000000000000000000000000000000000000000001p00000000000000000000000000001000000000000000000000000000000000000 = 36893488216138579967 % 1361129467683753853816604941579653742592
00000000000000000000000000000000000000000000000000000000000000001p00000000000000000000000000010000000000000000000000000000000000000 = 36893488284858056703 % 1361129467683753853816604941579653742592
00000000000000000000000000000000000000000000000000000000000000001p00000000000000000000000000100000000000000000000000000000000000000 = 36893488422297010175 % 1361129467683753853816604941579653742592
00000000000000000000000000000000000000000000000000000000000000001p00000000000000000000000001000000000000000000000000000000000000000 = 36893488697174917119 % 1361129467683753853816604941579653742592
00000000000000000000000000000000000000000000000000000000000000001p00000000000000000000000010000000000000000000000000000000000000000 = 36893489246930731007 % 1361129467683753853816604941579653742592
00000000000000000000000000000000000000000000000000000000000000001p00000000000000000000000100000000000000000000000000000000000000000 = 36893490346442358783 % 1361129467683753853816604941579653742592
00000000000000000000000000000000000000000000000000000000000000001p00000000000000000000001000000000000000000000000000000000000000000 = 36893492545465614335 % 1361129467683753853816604941579653742592
00000000000000000000000000000000000000000000000000000000000000001p00000000000000000000010000000000000000000000000000000000000000000 = 36893496943512125439 % 1361129467683753853816604941579653742592
00000000000000000000000000000000000000000000000000000000000000001p00000000000000000000100000000000000000000000000000000000000000000 = 36893505739605147647 % 1361129467683753853816604941579653742592
00000000000000000000000000000000000000000000000000000000000000001p00000000000000000001000000000000000000000000000000000000000000000 = 36893523331791192063 % 1361129467683753853816604941579653742592
00000000000000000000000000000000000000000000000000000000000000001p00000000000000000010000000000000000000000000000000000000000000000 = 36893558516163280895 % 1361129467683753853816604941579653742592
00000000000000000000000000000000000000000000000000000000000000001p00000000000000000100000000000000000000000000000000000000000000000 = 36893628884907458559 % 1361129467683753853816604941579653742592
00000000000000000000000000000000000000000000000000000000000000001p00000000000000001000000000000000000000000000000000000000000000000 = 36893769622395813887 % 1361129467683753853816604941579653742592
00000000000000000000000000000000000000000000000000000000000000001p00000000000000010000000000000000000000000000000000000000000000000 = 36894051097372524543 % 1361129467683753853816604941579653742592
00000000000000000000000000000000000000000000000000000000000000001p00000000000000100000000000000000000000000000000000000000000000000 = 36894614047325945855 % 1361129467683753853816604941579653742592
00000000000000000000000000000000000000000000000000000000000000001p00000000000001000000000000000000000000000000000000000000000000000 = 36895739947232788479 % 1361129467683753853816604941579653742592
00000000000000000000000000000000000000000000000000000000000000001p00000000000010000000000000000000000000000000000000000000000000000 = 36897991747046473727 % 1361129467683753853816604941579653742592
00000000000000000000000000000000000000000000000000000000000000001p00000000000100000000000000000000000000000000000000000000000000000 = 36902495346673844223 % 1361129467683753853816604941579653742592
00000000000000000000000000000000000000000000000000000000000000001p00000000001000000000000000000000000000000000000000000000000000000 = 36911502545928585215 % 1361129467683753853816604941579653742592
00000000000000000000000000000000000000000000000000000000000000001p00000000010000000000000000000000000000000000000000000000000000000 = 36929516944438067199 % 1361129467683753853816604941579653742592
00000000000000000000000000000000000000000000000000000000000000001p00000000100000000000000000000000000000000000000000000000000000000 = 36965545741457031167 % 1361129467683753853816604941579653742592
00000000000000000000000000000000000000000000000000000000000000001p00000001000000000000000000000000000000000000000000000000000000000 = 37037603335494959103 % 1361129467683753853816604941579653742592
00000000000000000000000000000000000000000000000000000000000000001p00000010000000000000000000000000000000000000000000000000000000000 = 37181718523570814975 % 1361129467683753853816604941579653742592
00000000000000000000000000000000000000000000000000000000000000001p00000100000000000000000000000000000000000000000000000000000000000 = 37469948899722526719 % 1361129467683753853816604941579653742592
00000000000000000000000000000000000000000000000000000000000000001p00001000000000000000000000000000000000000000000000000000000000000 = 38046409652025950207 % 1361129467683753853816604941579653742592
00000000000000000000000000000000000000000000000000000000000000001p00010000000000000000000000000000000000000000000000000000000000000 = 39199331156632797183 % 1361129467683753853816604941579653742592
00000000000000000000000000000000000000000000000000000000000000001p00100000000000000000000000000000000000000000000000000000000000000 = 41505174165846491135 % 1361129467683753853816604941579653742592
00000000000000000000000000000000000000000000000000000000000000001p01000000000000000000000000000000000000000000000000000000000000000 = 46116860184273879039 % 1361129467683753853816604941579653742592
00000000000000000000000000000000000000000000000000000000000000001p10000000000000000000000000000000000000000000000000000000000000000 = 55340232221128654847 % 1361129467683753853816604941579653742592
00000000000000000000000000000000000000000000000000000000000000010p00000000000000000000000000000000000000000000000000000000000000001 = 73786976294838206463 % 1361129467683753853816604941579653742592
*Main>

Fractals/Iterations in the complex plane/p misiurewicz

names

introduction

shifting q digits in blocks of b digits

$q=5\ {\text{and}}\ b=1$

$q=5\ {\text{and}}\ b=2$

$q=5\ {\text{and}}\ b=3$

$q=5\ {\text{and}}\ b=4$

Algorithm

input and output

steps

Examples

1/3

1/4

Code

Haskell code

References

See also