Fractals/Iterations in the complex plane/jlamination

< Fractals < Iterations in the complex plane

Here doubling map is used to analyze dynamics of complex quadratic polynomials. It is dynamical system easier to analyze then complex quadratic map.

Periodic orbits of angles under doubling map

Note that here chord joining 2 points z1 and z2 on unit circle means that $z_{2}=z_{1}^{2}$ . It does not mean that these points are landing points of the same ray.

Some orbits do not cross :

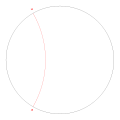Period 2 orbit ( angles under doubling map)
Period 3 orbit ( angles under doubling map)
Period 4 orbit ( angles under doubling map)
Period 5 orbit ( angles under doubling map)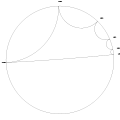
Period 6 orbit ( angles under doubling map)

but some do :

Period 6 orbit of 11/63 under doubling map
Period 9 orbit of 74/511 under doubling map

Orbit portraits

An orbit portrait can be in two forms:

list of lists of numbers (common fractions with even denominator)
image showing rays landing on periodic z points (= partition of dynamic plane)

Note that :

here chord joining 2 points z1 and z2 on unit circle means that these points are landing points of the same ray. It does not mean that $z_{2}=z_{1}^{2}$ .
An orbit portrait is a portrait of orbit, which is periodic under complex quadratic map.
The Julia set has many periodic orbits so it also hase many orbit portraits
An orbit portrait is combinatorial description of orbit
(Douady and Hubbard). Every repelling and parabolic periodic point of a quadratic polynomial fc is the landing point of an external ray with rational angle. Conversely, every external ray with rational angle lands either at a periodic or preperiodic point in J(fc ).^[1]

Image

Image can be made in three forms :

image of dynamic plane with Julia set and external rays landing on periodic orbit
sketch of above image made in :
- standard way : points of orbit are drawn inside unit circle and rays are made by lines joining angle ( point on unit circle) and point of orbit. It looks like sketch of above image
- hyperbolic way : points are on unit circle and here chord joining 2 points z1 and z2 on unit circle means that these points are landing points of the same ray. It does not mean that $z_{2}=z_{1}^{2}$ . Chord is drawn using arc ( part of orthogonal circle ).

Lamination of Julia sets

"Laminations were introduced to the context of polynomial dynamics in the early 1980’s by Thurston"^[2] Are used to show the landing pattern of external rays.

The lamination L gives :

a combinatorial description of the dynamics of quadratic map.^[3] because action of doubling map on the unit circle is a model of action of complex polynomial on complex plane^[4]
exact topological structure of Julia sets ^[5] = topological model for Julia set
the model of ray portraits. The external rays for angles in a lamination land at "cut points" of the Julia set / Mandelbrot set.

Note that here chord joining 2 points z1 and z2 on unit circle means that these points are landing points of the same ray. It does not mean that $z_{2}=z_{1}^{2}$ .

For a quadratic polynomials initial set has a form :^[6]

$\left\{\theta ,\theta +{\frac {1}{2}}\right\rbrace$

?????

Definition

Laminations of the unit disk in the plane is a closed collection of chords (leaves, arcs ) inside the unit disk

quadratic laminations = those that remain invariant under the angle doubling map ^[7]

Notation

chord = leaf = continuous path on the unit disc identifying (connecting) two points on the unit circle
pullback = a pullback process = backward iteration

Properities of lamination

Lamination must satisfy the following rules :

leaves do not cross, although thay may share endpoints
lamination is forward and backward invariant (under doubling map)

Invariance of lamination

"Invariance of a lamination L in the unit disc means that:

whenever there is a leaf of L joining $z_{1}$ and $z_{2}$ , there is also a leaf of L joining $z_{1}^{2}$ and $z_{2}^{2}$
whenever there is a chord joining $z_{1}$ and $z_{2}$ , there are points $\pm z_{3}^{2}$ and $\pm z_{4}^{2}$ with $z_{3}^{2}=z_{1}$ and $z_{4}^{2}=z_{2}$ , and such that there are leaves of L joining z3 to z4 , and −z3 to −z4 ."^[8]

Tools

Tools used to study dynamics of lamiantions :

Central Strip Lemma ^[9]

Drawing lamination

Drawlam : program for rendering laminations by Clinton P. Curry ^[10]. This program is licensed under a modified BSD-style license. It uses input file or reads from console.
Invariant lamination calculator Java applet by Danny Calegari. It computes the invariant lamination for a connected Julia set on the boundary of the Mandelbrot set with variable external angle. With Java src code
lamination by Danny Calegari. Cpp program for X11 using uses standard Xlib stuff. Source code is released under the terms of the GNU GPL. This program is a toy to do experiments with laminations of the circle. Represents it symbolically and pictorially. It needs only one input : the size of the lamination ( the number of endpoints of polygons). This set of endpoints is enumerated from 0 to size-1 in anticlockwise order. For each endpoint, the nextleaf points to the adjacent endpoint in the anticlockwise direction.

I have changed in main.cc :

#include <math.h>
#include <iostream> // I have removed .h
#include <stdlib.h>
#include "graphics.cc"
using namespace std; // added because : main.cc:101: error: ‘cout’ was not declared in this scope

and then in program directory :

make
./lamiantion

Examples

cut points of order 2

period one orbit = fixed point

For complex quadratic polynomials $f_{c}(z)$ for all parameters c in wake bounded by rays 1/3 and 2/3 there is repelling fixed point with orbit portrait :

${\mathcal {P}}({\mathcal {O}})=\left\{{\mathcal {A}}_{1}\right\rbrace =\left\{\left({\frac {1}{3}},{\frac {2}{3}}\right)\right\rbrace$

External rays landing on fixed point alpha
Paritition of the circle by 2 rays landing on period 1 orbit ( angles under doubling map)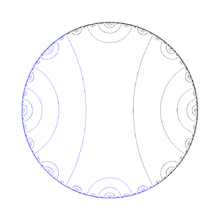
quadratic invariant lamination $L_{\frac {1}{3}}$ associated with basilica Julia set $f_{c}(z)=z^{2}-1$
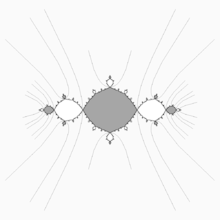Rays landing on cut points

cut points of order 3

period one orbit = fixed point

Orbit under quadratic map consists of one ( fixed point) :

${\mathcal {O}}=\left\{z_{1}\right\rbrace =\left\{\alpha _{c}\right\rbrace$

This point is a landing point of 3 external rays and has orbit portrait :

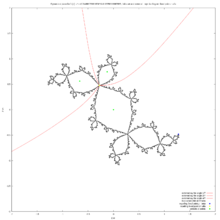${\mathcal {P}}({\mathcal {O}})=\left\{{\mathcal {A}}_{1}\right\rbrace =\left\{\left({\frac {1}{7}},{\frac {2}{7}},{\frac {4}{7}}\right)\right\rbrace$

Paritition of dynamic plane : Douady rabbit Julia set and external rays landing on fixed point $\alpha _{c}\,$
Orbit portrait made in hyperbolic way. Paritition of the circle by period 3 orbit ( angles under doubling map)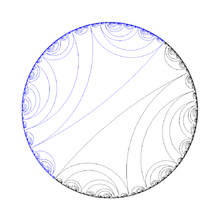
Lamination $L_{\frac {1}{7}}$ associated with rabbit Julia set

period 2 orbit

c is a root point of Mandelbrot set between period 2 and 6 components :^[11]

$c=-1+{\frac {1}{4}}e^{2\pi i{\frac {2}{3}}}\in \partial M$

with internal address 1-2-6.

Six periodic cycle of rays is landing on two-periodic parabolic orbit :

${\mathcal {O}}=\left\{z_{2,1},z_{2,2}\right\rbrace$

where :

$z_{2,1}=-{\frac {1}{2}}+{\frac {1}{2}}{\sqrt {1-e^{2\pi i{\frac {2}{3}}}}}$

$z_{2,2}=-{\frac {1}{2}}-{\frac {1}{2}}{\sqrt {1-e^{2\pi i{\frac {2}{3}}}}}$

with orbit portrait :

${\mathcal {P}}({\mathcal {O}})=\left\{{\mathcal {A}}_{1},{\mathcal {A}}_{2}\right\rbrace =\left\{\left({\frac {22}{63}},{\frac {25}{63}},{\frac {37}{63}}\right),\left({\frac {44}{63}},{\frac {50}{63}},{\frac {11}{63}}\right),\right\rbrace$

Paritition of parameter plane by rays landing on root point with internal adress 1-2-6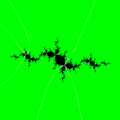
Paritition of dynamic plane by rays landing on parabolic orbit
Paritition of the circle by period 6 orbit ( angles under doubling map)

period 3 orbit

Parameter c is a center of period 9 hyperbolic component of Mandelbrot set

$c=-0.03111+0.79111*i$

Orbit under quadratic map consists of 3 points :

${\mathcal {O}}=\left\{z_{3,1},z_{3,2},z_{3,1}\right\rbrace$

orbit portrait associated with parabolic period 3 orbit ${\mathcal {O}}$ is :^[12]

${\mathcal {P}}({\mathcal {O}})=\left\{{\mathcal {A}}_{1},{\mathcal {A}}_{2},{\mathcal {A}}_{3}\right\rbrace =\left\{\left({\frac {74}{511}},{\frac {81}{511}},{\frac {137}{511}}\right),\left({\frac {148}{511}},{\frac {162}{511}},{\frac {274}{511}}\right),\left({\frac {296}{511}},{\frac {324}{511}},{\frac {37}{511}}\right)\right\rbrace$

Valence = 3 rays per orbit point ( = each point is a landing point of 3 external rays )

Rays for above angles land on points of that orbit .

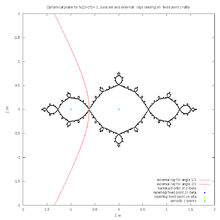
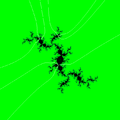Paritition of dynamic plane : Julia set and external rays landing on period 3 orbit
Orbit of 74/511 under doubling map

cut points of order 5

period one orbit = fixed point

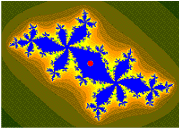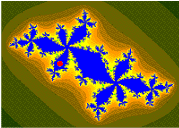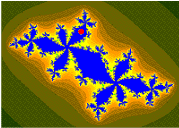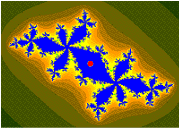cycle 5 superattracting orbit = c is a center of period 5 component orbit : {5/31 , 10/31 , 20/31 , 9/31 , 18/31}
orbit : {5/31 , 10/31 , 20/31 , 9/31 , 18/31}, crossing
orbit of 1/31 under doubling map, non crossing, = {1/31 , 2/31 , 4/31 , 8/31 , 16/31}. Parameter c will be on the parabolic point with internal angle 2/5

Questions

How to compute orbit portraits ?
How orbit portrait changes when I move inside Mandelbrot set ?
CRITERION FOR RAYS LANDING TOGETHER by JINSONG ZENG

References

↑ Towards classification of laminations associated to quadratic polynomials A Dissertation, Presented by Carlos Cabrera
↑ [COMBINATORICS AND TOPOLOGY OF STRAIGHTENING MAPS I : COMPACTNESS AND BIJECTIVITY HIROYUKI INOU AND JAN KIWI]
↑ Cubic Critical Portraits and Polynomials with Wandering Gaps Authors: A. Blokh, C. Curry, L. Oversteegen
↑ Mayer, J. , 2010-08-05 "Pullback Laminations" Paper presented at the annual meeting of the The Mathematical Association of America MathFest, Omni William Penn, Pittsburgh, PA
↑ THE SOLAR JULIA SETS OF BASIC QUADRATIC CREMER POLYNOMIALS by A. BLOKH, X. BUFF, A. CHERITAT, AND L. OVERSTEEGEN
↑ CUBIC CRITICAL PORTRAITS AND POLYNOMIALS WITH WANDERING GAPS by ALEXANDER BLOKH, CLINTON CURRY, AND LEX OVERSTEEGEN
↑ Houghton, Jeffrey. "Useful Tools in the Study of Laminations" Paper presented at the annual meeting of the The Mathematical Association of America MathFest, Omni William Penn, Pittsburgh, PA, Aug 05, 2010
↑ MULTIPLE EQUIVALENT MATINGS WITH THE AEROPLANE POLYNOMIAL byMARY REES
↑ Houghton, Jeffrey. "Useful Tools in the Study of Laminations" Paper presented at the annual meeting of the The Mathematical Association of America MathFest, Omni William Penn, Pittsburgh, PA, Aug 05, 2010
↑ Drawlam : program for rendering laminations by Clinton P. Curry
↑ Trees of visible components in the Mandelbrot set by Virpi K a u k o
↑ Boundaries of Bounded Fatou Components of Quadratic Maps Ross Flek and Linda Keen

Lamination for z2 + i from gallery of images by Curtis T McMullen
Invariant Factors, Julia Equivalences and the (Abstract) Mandelbrot Set by Karsten Keller. Book from series Lecture Notes in Mathematics

Volume 1732, 2000, DOI: 10.1007/BFb0103999. Springer-Verlag, Berlin-Heidelberg-NewYork 2000

This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

Fractals/Iterations in the complex plane/jlamination

Periodic orbits of angles under doubling map

Orbit portraits

Image

Lamination of Julia sets

Definition

Notation

Properities of lamination

Invariance of lamination

Tools

Drawing lamination

Examples

cut points of order 2

period one orbit = fixed point

cut points of order 3

period one orbit = fixed point

period 2 orbit

period 3 orbit

cut points of order 5

period one orbit = fixed point

Questions

See also

References