Fractals/Iterations in the complex plane/def cqp
< Fractals < Iterations in the complex planeDefinitions
Address
Internal
Internal addresses describe the combinatorial structure of the Mandelbrot set.[1]
Internal address :
- is not constant within hyperbolic component. Example : internal address of -1 is 1->2 and internal address of 0.9999 is 1[2]
- of hyperbolic component is defined as a internal address of it's center
angled
Angled internal address is an extension of internal address
Angle
Types of angle
| external angle | internal angle | plain angle | |
|---|---|---|---|
| parameter plane | |||
| dynamic plane | |||
where :
- is a multiplier map
- is a Boettcher function
external
The external angle is a angle of point of set's exterior. It is the same on all points on the external ray
internal
The internal angle[3] is an angle of point of component's interior
- it is a rational number and proper fraction measured in turns
- it is the same for all point on the internal ray
- in a contact point ( root point ) it agrees with the rotation number
- root point has internal angle 0
plain
The plain angle is an agle of complex point = it's argument [4]
Units
- turns
- degrees
- radians
Number types
Angle ( for example external angle in turns ) can be used in different number types
Examples :
the external arguments of the rays landing at z = −0.15255 + 1.03294i are :[5]
where :
Bifurcation
- Numerical Bifurcation Analysis of Maps
- MatCont[6]
Coordinate
- Fatou coordinate for every repelling and attracting petal ( linearization of function near parabolic fixed point )
- Boettcher
- Koenigs
Curves
Types:
- topology:
- closed versus open
- simple versus not simple
- other properities:
- invariant
- critical
Description[7]
- plane curve = it lies in a plane.
- closed = it starts and ends at the same place.
- simple = it never crosses itself.
closed
Closed curves are curves whose ends are joined. Closed curves do not have end points.
- Simple Closed Curve : A connected curve that does not cross itself and ends at the same point where it begins. It divides the plane into exactly two regions ( Jordan curve theorem ). Examples of simple closed curves are ellipse, circle and polygons.[8]
- complex Closed Curve ( not simple = non-simple ) It divides the plane into more than two regions. Example : Lemniscates.
"non-self-intersecting continuous closed curve in plane" = "image of a continuous injective function from the circle to the plane"
Circle
Unit circle
Unit circle is a boundary of unit disk[9]
where coordinates of point of unit circle in exponential form are :
Critical curves
Diagrams of critical polynomials are called critical curves.[10]
These curves create skeleton of bifurcation diagram.[11] (the dark lines[12])
Escape lines
"If the escape radius is equal to 2 the contour lines have a contact point (c= -2) and cannot be considered as equipotential lines" [13]
Invariant
Types:
- topological
- shift invariants
examples :
- curve is invariant for the map f ( evolution function ) if images of every point from the curve stay on that curve[14][15][16]
- curve is invariant for a system of ordinary differential equations[17]
Isocurves
Equipotential lines
Equipotential lines = Isocurves of complex potential
"If the escape radius is greater than 2 the contour lines are equipotential lines" [18]
Jordan curve

Jordan curve = a simple closed curve that divides the plane into an "interior" region bounded by the curve and an "exterior" region containing all of the nearby and far away exterior points[19]
Lamination
Lamination of the unit disk is a closed collection of chords in the unit disc, which can intersect only in an endpoint of each on the boundary circle[20][21]
It is a model of Mandelbrot or Julia set.
A lamination, L, is a union of leaves and the unit circle which satisfies :[22]
- leaves do not cross (although they may share endpoints) and
- L is a closed set.
Leaf
Chords = leaves = arcs
A leaf on the unit disc is a path connecting two points on the unit circle. [23]
Open curve
Curve which is not closed. Examples : line, ray.
Ray
Rays are :
- invariant curves
- dynamic or parameter
- external or internal
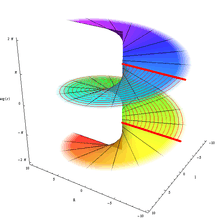
Internal ray
Internal rays are :
- dynamic ( on dynamic plane , inside filled Julia set )
- parameter ( on parameter plane , inside Mandelbrot set )
Spider
A spider S is a collection of disjoint simple curves called legs [24]( extended rays = external + internal ray) in the complex plane connecting each of the post-critical points to infnity [25]
See :
Vein
"A vein in the Mandelbrot set is a continuous, injective arc inside in the Mandelbrot set"
"The principal vein is the vein joining to the main cardioid" (Entropy, dimension and combinatorial moduli for one-dimensional dynamical systems. A dissertation by Giulio Tiozzo )
Discretization
discretization[26] and its reverse [27]
Dynamics
symbolic
"Symbolic dynamics encodes :
- a dynamical system by a shift map on a space of sequences over finite alphabet using Markov paritition of the space
- the points of space by their itineraries with respect to the paritition " ( Volodymyr Nekrashevych - Symbolic dynamics and self-similar groups
equation
differential
differential equations
- exact analytic solutions.
- approximated solution
- use perturbation theory to approximate the solutions
Function
Derivative
Derivative of Iterated function (map)
Derivative with respect to c
On parameter plane :
- is a variable
- is constant
This derivative can be found by iteration starting with
and then
This can be verified by using the chain rule for the derivative.
- Maxima CAS function :
dcfn(p, z, c) :=
if p=0 then 1
else 2*fn(p-1,z,c)*dcfn(p-1, z, c)+1;
Example values :
Derivative with respect to z
is first derivative with respect to c.
This derivative can be found by iteration starting with
and then :
Germ
Germ [31] of the function f in the neighborhood of point z is a set of the functions g which are indistinguishable in that neighborhood
See :
map
- differences between map and the function [32]
- Iterated function = map[33]
- an evolution function[34] of the discrete nonlinear dynamical system[35]
is called map :
types
Polynomial
Critical
Critical polynomial :
so
These polynomials are used for finding :
- centers of period n Mandelbrot set components. Centers are roots of n-th critical polynomials ( points where critical curve Qn croses x axis )
- Misiurewicz points
post-critically finite
a post-critically finite polynomial = all critical points have finite orbit
Resurgent
"resurgent functions display at each of their singular points a behaviour closely related to their behaviour at the origin. Loosely speaking, these functions resurrect, or surge up - in a slightly different guise, as it were - at their singularities"
J. Écalle, 1980[36]
glitches
glitches = Incorrect parts of renders[37] using perturbation techique
Invariants
sth is invariant with respect to the transformation = non modified, steady
Topological methods for the analysis of dynamical systems
Invariants type
- metric invariants
- dynamical invariants,
- topological invariants.
dynamical
Dynamical invariants = invariants of the dynamical system
- periodic points
- fixed point
- invariant curve
- periodic ray
- external
- internal
- periodic ray
Dynamical Invariants Derived from Recurrence Plots[38]
Interval
a partition of an interval into subintervals
- Markov paritition[39]
Iteration
Itinerary
is an itinerary of point x under the map f relative to the paritirtion.
It is a right-infinite sequence of zeros and ones [40]
where
Examples :
For rotation map and invariant interval ( circle ) :
one can compute :
and split interval into 2 subintervals ( lower circle paritition):
then compute s according to it's relation with critical point :
Itinerary can be converted[41] to point
Magnitude
magnitude of the point ( complex number in 2D case) = it's distance from the origin
Map
types
- The map f is hyperbolic if every critical orbit converges to a periodic orbit.[42]
Complex quadratic map
Forms
c form :
- math notation :
- Maxima CAS function :
f(z,c):=z*z+c;
(%i1) z:zx+zy*%i; (%o1) %i*zy+zx (%i2) c:cx+cy*%i; (%o2) %i*cy+cx (%i3) f:z^2+c; (%o3) (%i*zy+zx)^2+%i*cy+cx (%i4) realpart(f); (%o4) -zy^2+zx^2+cx (%i5) imagpart(f); (%o5) 2*zx*zy+cy
Iterated quadratic map
- math notation
...
or with subscripts :
- Maxima CAS function :
fn(p, z, c) :=
if p=0 then z
elseif p=1 then f(z,c)
else f(fn(p-1, z, c),c);
zp:fn(p, z, c);
lambda form :
More description Maxima CAS code ( here m not lambda is used ) :
(%i2) z:zx+zy*%i; (%o2) %i*zy+zx (%i3) m:mx+my*%i; (%o3) %i*my+mx (%i4) f:m*z+z^2; (%o4) (%i*zy+zx)^2+(%i*my+mx)*(%i*zy+zx) (%i5) realpart(f); (%o5) -zy^2-my*zy+zx^2+mx*zx (%i6) imagpart(f); (%o6) 2*zx*zy+mx*zy+my*zx
Switching between forms
Start from :
- internal angle
- internal radius r
Multiplier of fixed point :
When one wants change from lambda to c :[44]
or from c to lambda :
Example values :
| r | c | fixed point alfa | fixed point | ||
|---|---|---|---|---|---|
| 1/1 | 1.0 | 0.25 | 0.5 | 1.0 | 0 |
| 1/2 | 1.0 | -0.75 | -0.5 | -1.0 | 0 |
| 1/3 | 1.0 | 0.64951905283833*i-0.125 | 0.43301270189222*i-0.25 | 0.86602540378444*i-0.5 | 0 |
| 1/4 | 1.0 | 0.5*i+0.25 | 0.5*i | i | 0 |
| 1/5 | 1.0 | 0.32858194507446*i+0.35676274578121 | 0.47552825814758*i+0.15450849718747 | 0.95105651629515*i+0.30901699437495 | 0 |
| 1/6 | 1.0 | 0.21650635094611*i+0.375 | 0.43301270189222*i+0.25 | 0.86602540378444*i+0.5 | 0 |
| 1/7 | 1.0 | 0.14718376318856*i+0.36737513441845 | 0.39091574123401*i+0.31174490092937 | 0.78183148246803*i+0.62348980185873 | 0 |
| 1/8 | 1.0 | 0.10355339059327*i+0.35355339059327 | 0.35355339059327*i+0.35355339059327 | 0.70710678118655*i+0.70710678118655 | 0 |
| 1/9 | 1.0 | 0.075191866590218*i+0.33961017714276 | 0.32139380484327*i+0.38302222155949 | 0.64278760968654*i+0.76604444311898 | 0 |
| 1/10 | 1.0 | 0.056128497072448*i+0.32725424859374 | 0.29389262614624*i+0.40450849718747 | 0.58778525229247*i+0.80901699437495 |
One can easily compute parameter c as a point c inside main cardioid of Mandelbrot set :
of period 1 hyperbolic component ( main cardioid) for given internal angle ( rotation number) t using this c / cpp code by Wolf Jung[45]
double InternalAngleInTurns;
double InternalRadius;
double t = InternalAngleInTurns *2*M_PI; // from turns to radians
double R2 = InternalRadius * InternalRadius;
double Cx, Cy; /* C = Cx+Cy*i */
// main cardioid
Cx = (cos(t)*InternalRadius)/2-(cos(2*t)*R2)/4;
Cy = (sin(t)*InternalRadius)/2-(sin(2*t)*R2)/4;
or this Maxima CAS code :
/* conformal map from circle to cardioid ( boundary
of period 1 component of Mandelbrot set */
F(w):=w/2-w*w/4;
/*
circle D={w:abs(w)=1 } where w=l(t,r)
t is angle in turns ; 1 turn = 360 degree = 2*Pi radians
r is a radius
*/
ToCircle(t,r):=r*%e^(%i*t*2*%pi);
GiveC(angle,radius):=
(
[w],
/* point of unit circle w:l(internalAngle,internalRadius); */
w:ToCircle(angle,radius), /* point of circle */
float(rectform(F(w))) /* point on boundary of period 1 component of Mandelbrot set */
)$
compile(all)$
/* ---------- global constants & var ---------------------------*/
Numerator :1;
DenominatorMax :10;
InternalRadius:1;
/* --------- main -------------- */
for Denominator:1 thru DenominatorMax step 1 do
(
InternalAngle: Numerator/Denominator,
c: GiveC(InternalAngle,InternalRadius),
display(Denominator),
display(c),
/* compute fixed point */
alfa:float(rectform((1-sqrt(1-4*c))/2)), /* alfa fixed point */
display(alfa)
)$
Circle map
Circle map [46]
- irrational rotation[47]
Doubling map
definition [48]
C function ( using GMP library) :
// rop = (2*op ) mod 1
void mpq_doubling(mpq_t rop, const mpq_t op)
{
mpz_t n; // numerator
mpz_t d; // denominator
mpz_inits(n, d, NULL);
//
mpq_get_num (n, op); //
mpq_get_den (d, op);
// n = (n * 2 ) % d
mpz_mul_ui(n, n, 2);
mpz_mod( n, n, d);
// output
mpq_set_num(rop, n);
mpq_set_den(rop, d);
mpz_clears(n, d, NULL);
}
- Maxima CAS function using numerator and denominator as an input
doubling_map(n,d):=mod(2*n,d)/d $
or using rational number as an input
DoublingMap(r):=
block([d,n],
n:ratnumer(r),
d:ratdenom(r),
mod(2*n,d)/d)$
- Common Lisp function
(defun doubling-map (ratio-angle)
" period doubling map = The dyadic transformation (also known as the dyadic map,
bit shift map, 2x mod 1 map, Bernoulli map, doubling map or sawtooth map "
(let* ((n (numerator ratio-angle))
(d (denominator ratio-angle)))
(setq n (mod (* n 2) d)) ; (2 * n) modulo d
(/ n d))) ; result = n/d
- Haskell function[49]
-- by Claude Heiland-Allen
-- type Q = Rational
double :: Q -> Q
double p
| q >= 1 = q - 1
| otherwise = q
where q = 2 * p
- C++
// mndcombi.cpp by Wolf Jung (C) 2010.
// http://mndynamics.com/indexp.html
// n is a numerator
// d is a denominator
// f = n/d is a rational fraction ( angle in turns )
// twice is doubling map = (2*f) mod 1
// n and d are changed ( Arguments passed to function by reference)
void twice(unsigned long long int &n, unsigned long long int &d)
{ if (n >= d) return;
if (!(d & 1)) { d >>= 1; if (n >= d) n -= d; return; }
unsigned long long int large = 1LL;
large <<= 63; //avoid overflow:
if (n < large) { n <<= 1; if (n >= d) n -= d; return; }
n -= large;
n <<= 1;
large -= (d - large);
n += large;
}
Inverse function of doubling map
Every angle α ∈ R/Z measured in turns has :
- one image = 2α mod 1 under doubling map
- "two preimages under the doubling map: α/2 and (α + 1)/2." [50]. Inverse of doubling map is multivalued function.
In Maxima CAS :
InvDoublingMap(r):= [r/2, (r+1)/2];
Note that difference between these 2 preimages
is half a turn = 180 degrees = Pi radians.
Feigenbaum map
"the Feigenbaum map F is a solution of Cvitanovic-Feigenbaum equation"[51]
First return map
definition [52]
"In contrast to a phase portrait, the return map is a discrete description of the underlying dynamics. .... A return map (plot) is generated by plotting one return value of the time series against the previous one "[53]
"If x is a periodic point of period p for f and U is a neighborhood of x, the composition maps U to another neighborhood V of x. This locally defined map is the return map for x." ( W P Thurston : On the geometry and dynamics of Iterated rational maps)
"The first return map S → S is the map defined by sending each x0 ∈ S to the point of S where the orbit of x0 under the system first returns to S." [54]
"way to obtain a discrete time system from a continuous time system, called the method of Poincar´e sections Poincar´e sections take us from : continuous time dynamical systems on (n + 1)-dimensional spaces to discrete time dynamical systems on n-dimensional spaces"[55]
Multiplier map
Multiplier map gives an explicit uniformization of hyperbolic component by the unit disk :
Multiplier map is a conformal isomorphism.[56]
Rotation map
Rotation map describes counterclockwise rotation of point thru turns on the unit circle :
It is used for computing :
- rotation maps
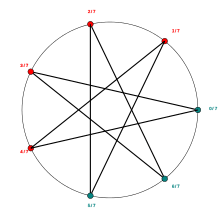
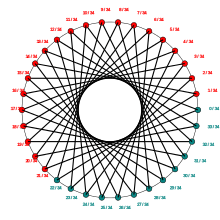
Shift map
names :
- bit shift map ( because it shifts the bit ) = if the value of an iterate is written in binary notation, the next iterate is obtained by shifting the binary point one bit to the right, and if the bit to the left of the new binary point is a "one", replacing it with a zero.
- 2x mod 1 map ( because it is math description of it's action )
Shift map (one-sided binary left shift ) acts on one-sided infinite sequence of binary numbers by
It just drops first digit of the sequence.
If we treat sequence as a binary fraction :
then shift map = the dyadic transformation = dyadic map = bit shift map= 2x mod 1 map = Bernoulli map = doubling map = sawtooth map
and "shifting N places left is the same as multiplying by 2 to the power N (written as 2N)"[57] ( operator << )
See also:
Multiplier
Multiplier of periodic z-point : [58]
Math notation :
Maxima CAS function for computing multiplier of periodic cycle :
m(p):=diff(fn(p,z,c),z,1);
where p is a period. It takes period as an input, not z point.
| period | ||
|---|---|---|
| 1 | ||
| 2 | ||
| 3 |
It is used to :
- compute stability index of periodic orbit ( periodic point) = ( where r is a n internal radius
- multiplier map
Number
Rotation number
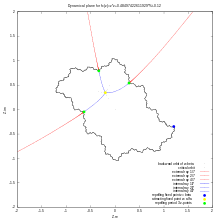
The rotation number[59][60][61][62][63] of the disk ( component) attached to the main cardioid of the Mandelbrot set is a proper, positive rational number p/q in lowest terms where :
- q is a period of attached disk ( child period ) = the period of the attractive cycles of the Julia sets in the attached disk
- p descibes fc action on the cycle : fc turns clockwise around z0 jumping, in each iteration, p points of the cycle [64]
Features :
- in a contact point ( root point ) it agrees with the internal angle
- the rotation numbers are ordered clockwise along the boundary of the componant
- " For parameters c in the p/q-limb, the filled Julia set Kc has q components at the fixed point αc . These are permuted cyclically by the quadratic polynomial fc(z), going p steps counterclockwise " Wolf Jung
Winding number
def[65]
Orbit
Orbit is a sequence of points = trajectory
Critical
Forward orbit[66] of a critical point[67][68] is called a critical orbit. Critical orbits are very important because every attracting periodic orbit[69] attracts a critical point, so studying the critical orbits helps us understand the dynamics in the Fatou set.[70][71] [72]
This orbit falls into an attracting periodic cycle.
Code :
"https://github.com/conanite/rainbow/blob/master/src/arc/rainbow/spiral.arc
This software is copyright (c) Conan Dalton 2008. Permission to use it is granted under the Perl Foundations's Artistic License 2.0.
This software includes software that is copyright (c) Paul Graham and Robert Morris, distributed under the Perl Foundations's Artistic License 2.0.
This software uses javacc which is copyright (c) its authors
"
(def plot (plt c)
(with (z 0+0i
n 0
repeats 0)
(while (and (small z) (< n 10000) (< repeats 1000))
(assign n (+ n 1)
z (+ c (* z z))
repeats (if (apply plt (complex-parts z))
(+ repeats 1)
0)))))
Here are images:
- images of critical orbitsat commons
- by Mike Croucher[73]
- Chris King [74]
- list : critical orbits
- images by Conan written in Rainbow
Forward
Homoclinic / heteroclinic
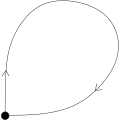 homoclinic orbit
homoclinic orbit Heteroclinic orbit
Heteroclinic orbit
Inverse
Inverse = Backward
Parameter
Parameter
- point of parameter plane : " is renormalizable if restriction of some of its iterate gives a polinomial-like map of the same or lower degree. " [75]
- parameter of the function
Paritition
- Markov
Period
The smallest positive integer value p for which this equality
holds is the period[76] of the orbit.[77]
is a point of periodic orbit ( limit cycle ) .
More is here
Perturbation
- Perturbation technque for fast rendering the deep zoom images of the Mandelbrot set[78]
- perturbation of parabolic point [79]
- use perturbation theory to approximate the solutions of the differential equations
Plane
Planes [80]
Douady’s principle : “sow in dynamical plane and reap in parameter space”.
Dynamic plane
- z-plane for fc(z)= z^2 + c
- z-plane for fm(z)= z^2 + m*z
Parameter plane
See :[81]
Types of the parameter plane :
- c-plane ( standard plane )
- exponential plane ( map) [82][83]
- flatten' the cardiod ( unroll ) [84][85] = "A region along the cardioid is continuously blown up and stretched out, so that the respective segment of the cardioid becomes a line segment. .." ( Figure 4.22 on pages 204-205 of The Science Of Fractal Images)[86]
- transformations [87]
 c-plane
c-plane inverted c plane = 1/c plane
inverted c plane = 1/c plane unrolled
unrolled
 lambda plane
lambda plane
Points
Band-merging
the band-merging points are Misiurewicz points[88]
Biaccessible
If there exist two distinct external rays landing at point we say that it is a biaccessible point. [89]
Center
Nucleus or center of hyperbolic component
A center of a hyperbolic component H is a parameter ( or point of parameter plane ) such that the corresponding periodic orbit has multiplier= 0." [90]
Synonyms :
- Nucleus of a Mu-Atom [91]
Center of Siegel Disc
Center of Siegel disc is a irrationally indifferent periodic point.
Mane's theorem :
"... appart from its center, a Siegel disk cannot contain any periodic point, critical point, nor any iterated preimage of a critical or periodic point. On the other hand it can contain an iterated image of a critical point." [92]
Critical
A critical point[93] of is a point in the dynamical plane such that the derivative vanishes:
Since
implies
we see that the only (finite) critical point of is the point .
is an initial point for Mandelbrot set iteration.[94]
Cut
Cut point k of set S is a point for which set S-k is dissconected ( consist of 2 or more sets).[95] This name is used in a topology.
Examples :
- root points of Mandelbrot set
- Misiurewicz points of boundary of Mandelbrot set
- cut points of Julia sets ( in case of Siegel disc critical point is a cut point )
These points are landing points of 2 or more external rays.
Point which is a landing point of 2 external rays is called biaccesible
Cut ray is a ray which converges to landing point of another ray. [96]
Cut rays can be used to construct puzzles.
Cut angle is an angle of cut ray.
fixed
Periodic point when period = 1
Feigenbaum

The Feigenbaum Point[97] is a :
- point c of parameter plane
- is the limit of the period doubling cascade of bifurcations
- an infinitely renormalizable parameter of bounded type
- boundary point between chaotic ( -2 < c < MF ) and periodic region ( MF< c < 1/4)[98]
Generalized Feigenbaum points are :
- the limit of the period-q cascade of bifurcations
- landing points of parameter ray or rays with irrational angles
Examples :
- -.1528+1.0397i)
The Mandelbrot set is conjectured to be self- similar around generalized Feigenbaum points[99] when the magnification increases by 4.6692 (the Feigenbaum Constant) and period is doubled each time[100]
n Period = 2^n Bifurcation parameter = cn Ratio 1 2 -0.75 N/A 2 4 -1.25 N/A 3 8 -1.3680989 4.2337 4 16 -1.3940462 4.5515 5 32 -1.3996312 4.6458 6 64 -1.4008287 4.6639 7 128 -1.4010853 4.6682 8 256 -1.4011402 4.6689 9 512 -1.401151982029 10 1024 -1.401154502237 infinity -1.4011551890 ...
Bifurcation parameter is a root point of period = 2^n component. This series converges to the Feigenbaum point c = −1.401155
The ratio in the last column converges to the first Feigenbaum constant.
" a "Feigenbaum point" (an infinitely renormalizable parameter of bounded type, such as the famous Feigenbaum value which is the limit of the period-2 cascade of bifurcations), then Milnor's hairiness conjecture, proved by Lyubich, states that rescalings of the Mandelbrot set converge to the entire complex plane. So there is certainly a lot of thickness near such a point, although again this may not be what you are looking for. It may also prove computationally intensive to produce accurate pictures near such points, because the usual algorithms will end up doing the maximum number of iterations for almost all points in the picture." Lasse Rempe-Gillen[101]
infinity
The point at infinity [102]" is a superattracting fixed point, but more importantly its immediate basin of attraction - that is, the component of the basin containing the fixed point itself - is completely invariant (invariant under forward and backwards iteration). This is the case for all polynomials (of degree at least two), and is one of the reasons that studying polynomials is easier than studying general rational maps (where e.g. the Julia set - where the dynamics is chaotic - may in fact be the whole Riemann sphere). The basin of infinity supports foliations into "external rays" and "equipotentials", and this allows one to study the Julia set. This idea was introduced by Douady and Hubbard, and is the basis of the famous "Yoccoz puzzle"." Lasse Rempe-Gillen[103]
Misiurewicz
Misiurewicz point[104] = " parameters where the critical orbit is pre-periodic.
Examples are:
- band-merging points of chaotic bands (the separator of the chaotic bands Bi−1 and Bi )[105]
- the branch points
- tips in the Mandelbrot set ( tips of the midgets ) [106]
Characteristic Misiurewicz pointof the chaotic band of the Mandelbrot set is :[107]
- the most prominent and visible Misiurewicz point of a chaotic band
- have the same period as the band
- have the same period as the gene of the band
Myrberg-Feigenbaum
MF = the Myrberg-Feigenbaum point is the different name for the Feigenbaum Point.
Parabolic point
parabolic points : this occurs when two singular points coallesce in a double singular point (parabolic point)[108]
Periodic
Point z has period p under f if :
Pinching
"Pinching points are found as the common landing points of external rays, with exactly one ray landing between two consecutive branches. They are used to cut M or K into well-defined components, and to build topological models for these sets in a combinatorial way. " ( definition from Wolf Jung program Mandel )
See for examples :
- period 2 = Mandel, demo 2 page 3.
- period 3 = Mandel, demo 2 page 5 [109]
post-critical
A post-critical point is a point
where is a critical point. [110]
precritical
precritical points, i.e., the preimages of 0
root
The root point :
- has a rotational number 0
- it is a biaccesible point ( landing point of 2 external rays )
singular
the singular points of a dynamical system
In complex analysis there are four classes of singularities:
- Isolated singularities: Suppose the function f is not defined at a, although it does have values defined on U \ {a}.
- The point a is a removable singularity of f if there exists a holomorphic function g defined on all of U such that f(z) = g(z) for all z in U \ {a}. The function g is a continuous replacement for the function f.
- The point a is a pole or non-essential singularity of f if there exists a holomorphic function g defined on U with g(a) nonzero, and a natural number n such that f(z) = g(z) / (z − a)n for all z in U \ {a}. The least such number n is called the order of the pole. The derivative at a non-essential singularity itself has a non-essential singularity, with n increased by 1 (except if n is 0 so that the singularity is removable).
- The point a is an essential singularity of f if it is neither a removable singularity nor a pole. The point a is an essential singularity if and only if the Laurent series has infinitely many powers of negative degree.
- Branch points are generally the result of a multi-valued function, such as or being defined within a certain limited domain so that the function can be made single-valued within the domain. The cut is a line or curve excluded from the domain to introduce a technical separation between discontinuous values of the function. When the cut is genuinely required, the function will have distinctly different values on each side of the branch cut. The shape of the branch cut is a matter of choice, however, it must connect two different branch points (like and for ) which are fixed in place.
Portrait
orbit portrait
types
There are two types of orbit portraits: primitive and satellite. [111]If is the valence of an orbit portrait and is the recurrent ray period, then these two types may be characterized as follows:
- Primitive orbit portraits have and . Every ray in the portrait is mapped to itself by . Each is a pair of angles, each in a distinct orbit of the doubling map. In this case, is the base point of a baby Mandelbrot set in parameter space.
- Satellite ( non-primitive ) orbit portraits have . In this case, all of the angles make up a single orbit under the doubling map. Additionally, is the base point of a parabolic bifurcation in parameter space.
Processes and phenomenona
Contraction and dilatation
- the contraction z → z/2
- the dilatation z → 2z.
Implosion and explosion

Implosion is :
- the process of sudden change of quality fuatures of the object, like collapsing (or being squeezed in)
- the opposite of explosion
Example : parabolic implosion in complex dynamics, when filled Julia for complex quadratic polynomial set looses all its interior ( when c goes from 0 along internal ray 0 thru parabolic point c=1/4 and along extrnal ray 0 = when c goes from interior , crosses the bounday to the exterior of Mandelbrot set)[112]
Explosion is a :
- is a sudden change of quality fuatures of the object in an extreme manner,
- the opposite of implosion
Example : in exponential dynamics when λ> 1/e , the Julia set of is the entire plane.[113]
Tuning
Radius
Conformal radius
Conformal radius of Siegel Disk [115][116]
Escape radius ( ER)
Escape radius ( ER ) or bailout value is a radius of circle target set used in bailout test
Minimal Escape Radius should be grater or equal to 2 :
Better estimation is :[117][118]
Inner radius
Inner radius of Siegel Disc
- radius of inner circle, where inner circle with center at fixed point is the biggest circle inside Siegel Disc.
- minimal distance between center of Siel Disc and critical orbit
Internal radius
Internal radius is a:
- absolute value of multiplier
Sequences
A sequence is an ordered list of objects (or events).[119]
A series is the sum of the terms of a sequence of numbers.[120] Some times these names are not used as in above definitions.
Orbit
Orbit can be:
Set
Continuum
definition[121]
Component
Components of parameter plane
mu-atom , ball, bud, bulb, decoration, lake and lakelet.[122]
Islands
Names :
- mini Mandelbrot set
- 'baby'-Mandelbrot set
- island mu-molecules = embedded copy of the Mandelbrot Set[123]
- Bug
- Island
- Mandelbrotie
- Midget
List of islands :
- http://mrob.com/pub/mu-data/largest-islands.txt
- http://mrob.com/pub/muency/largestislands.html
- http://www.math.cornell.edu/~rperez/Documents/maximals.pdf
- http://fraktal.republika.pl/mset_external_ray_mini.html
- http://mathr.co.uk/mandelbrot/feature-database.csv.bz2 ( a database of all islands up to period 16, found by tracing external rays): period, islandhood, angled internal address, lower external angle numerator, denominator, upper numerator, denominator, orientation, size, centre realpart, imagpart
Primary and satellite
"Hyperbolic components come in two kinds, primitive and satellite, depending on the local properties of their roots." [124]
Child (Descendant ) and the parent
def [125]
Hyperbolic component of Mandelbrot set
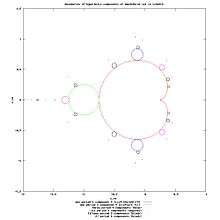
Domain is an open connected subset of a complex plane.
"A hyperbolic component H of Mandelbrot set is a maximal domain (of parameter plane) on which has an attracting periodic orbit.
A center of a H is a parameter ( or point of parameter plane ) such that the corresponding periodic orbit has multiplier= 0." [126]
A hyperbolic component is narrow if it contains no component of equal or lesser period in its wake [127]
features of hyperbolic component
- period
- islandhood ( shape = cardiod or circle )
- angled internal address
- lower and upper external angle of rays landing on it's root
- center (
- root
- orientation
- size
Limb

p/q limb is a part of Mandelbrot set contained inside p/q wake
Wake
Wake is the region of parameter plane enclosed by two external rays landing on the same root point on the boundary of main cardioid ( period 1 hyperbolic component).
Angles of the external rays that land on the root point one can find by :
- Combinatorial algorithm = Devaney's method
- book program by Claude Heiland-Allen
- wake function from program Mandel by Wolf Jung
Components of dynamical plane
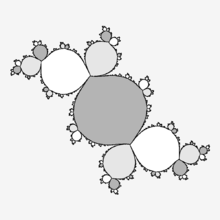 Components of interior of Filled Julia set
Components of interior of Filled Julia set Inverse iteration of Siegel disc component
Inverse iteration of Siegel disc component
In case of Siegel disc critical orbit is a boundary of component containing Siegel Disc.
Domain
Domain in mathematical analysis it is an open connected set
Jordan domain
"A Jordan domain[128] J is the the homeomorphic image of a closed disk in E2. The image of the boundary circle is a Jordan curve, which by the Jordan Curve Theorem separates the plane into two open domains, one bounded, the other not, such that the curve is the boundary of each." [129]
Dwell bands
"Dwell bands are regions where the integer iteration count is constant, when the iteration count decreases (increases) by 1 then you have passed a dwell band going outwards (inwards). " [130] Other names:
- level sets of integer escape time
Flower
Invariant
"A subset S of the domain Ω is an invariant set for the system (7.1) if the orbit through a point of S remains in S for all t ∈ R. If the orbit remains in S for t > 0, then S will be said to be positively invariant. Related definitions of sets that are negatively invariant, or locally invariant, can easily be given" [131]
Examples :
- invariant point = fixed point
- invariant cycle = periodic point
- invariant circle
- petal = invariant planar set
Level set
- a level set of a real-valued function f[132] ( see also dwell band)
- Level set methods (LSM)
Planar set
a non-separating planar set is a set whose complement in the plane is connected.[133]
Sepal
Target set
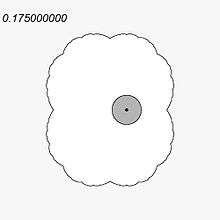
Elliptic case
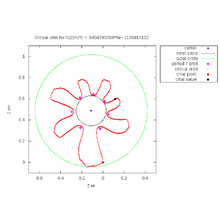
For the elliptic dynamics, when there is a Siegel disc, the target set is an inner circle
Hyperbolic case
Infinity is allways hyperbolic attractor for forward iteration of polynomials. Target set here is an exterior of any shape containing all point of Julia set ( and it's interior). There are also other hyperbolic attractors.
In case of forward iteration target set is an arbitrary set on dynamical plane containing infinity and not containing points of filled Julia set.
For escape time algorithms target set determines the shape of level sets and curves. It does not do it for other methods.
Exterior of circle
This is typical target set. It is exterior of circle with center at origin and radius =ER :
Radius is named escape radius ( ER ) or bailout value.
Circle of radius=ER centered at the origin is :
Exterior of square
Here target set is exterior of square of side length centered at origin
Parabolic case : petal

In the parabolic case target set shoul be iside petal
Trap
Trap is an another name of the target set. It is a set which captures any orbit tending to point inside the trap ( fixed / periodic point ).
Surgery
- surgery in differential topology [134]
 Surgery on the circle
Surgery on the circle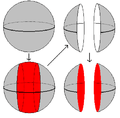 Surgery on the sphere
Surgery on the sphere
Links:
Test
Bailout test or escaping test

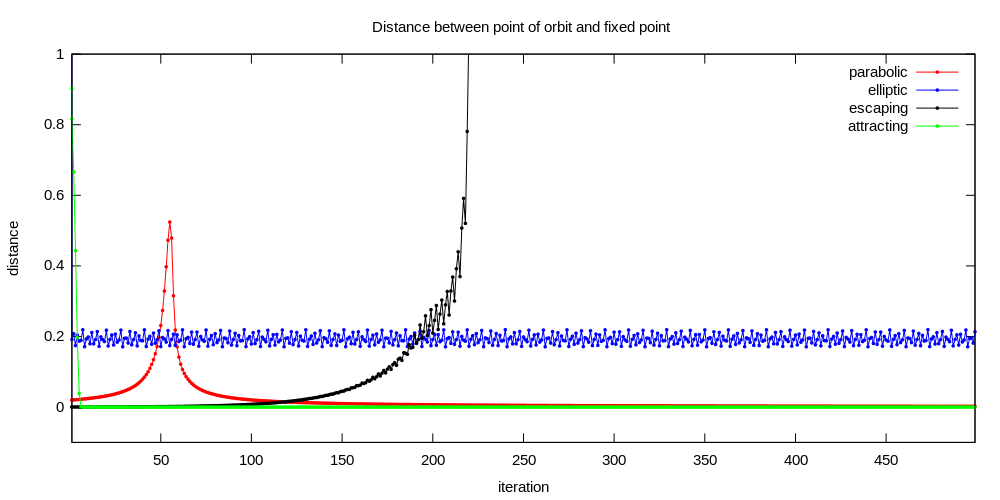
It is used to check if point z on dynamical plane is escaping to infinity or not.[135] It allows to find 2 sets :
- escaping points ( it should be also the whole basing of attraction to infinity)[136]
- not escaping points ( it should be the complement of basing of attraction to infinity)
In practice for given IterationMax and Escape Radius :
- some pixels from set of not escaping points may contain points that escape after more iterations then IterationMax ( increase IterMax )
- some pixels from escaping set may contain points from thin filaments not choosed by maping from integer to world ( use DEM )
If is in the target set then is escaping to infinity ( bailouts ) after n forward iterations ( steps).[137]
The output of test can be :
- boolean ( yes/no)
- integer : integer number (value of the last iteration)
Tree
Farey tree
Farey tree = Farey sequence as a tree
Hubbard tree
"Hubbard trees are finite planar trees, equipped with self-maps, which classify postcritically finite polynomials as holomorphic dynamical systems on the complex plane." [138]
References
- ↑ Rational Maps with Clustering and the Mating of Polynomials by Thomas Joseph Sharland
- ↑ Topics from One-Dimensional Dynamics by Karen M. Brucks,Henk Bruin. page 265 exercise 14.2.12
- ↑ muency - internal angle ( the Mandelbrot Set Glossary and Encyclopedia, by Robert Munafo, (c) 1987-2016. )
- ↑ argument of complex number
- ↑ A Method to Solve the Limitations in Drawing External Rays of the Mandelbrot Set M. Romera, G. Pastor, A. B. Orue, A. Martin, M.-F. Danca, and F. Montoya
- ↑ Matcont - is a Matlab software project for the numerical continuation and bifurcation study of continuous and discrete parameterized dynamical systems. Leaders of the project are Willy Govaerts (Gent,B) and Yuri A. Kuznetsov (Utrecht,NL).
- ↑ geometry by Dr. Carol JVF Burns
- ↑ What is a Curve ?
- ↑ Unit circle in wikipedia
- ↑ The Road to Chaos is Filled with Polynomial Curves by Richard D. Neidinger and R. John Annen III. American Mathematical Monthly, Vol. 103, No. 8, October 1996, pp. 640-653
- ↑ Hao, Bailin (1989). Elementary Symbolic Dynamics and Chaos in Dissipative Systems. World Scientific. ISBN 9971-5-0682-3. http://power.itp.ac.cn/~hao/.
- ↑ M. Romera, G. Pastor and F. Montoya, "Misiurewicz points in one-dimensional quadratic maps", Physica A, 232 (1996), 517-535. Preprint
- ↑ Escape lines versus equipotential lines in the Mnadelbrot set by M. Romera, Pastor G , D. de la Guía, Montoya
- ↑ The Computation of Invariant Circles of Maps Article in Physica D Nonlinear Phenomena 16(2):243-251 · June 1985 DOI: 10.1016/0167-2789(85)90061-2 1st I.G. Kevrekidis
- ↑ A Newton-Raphson method for numerically constructing invariant curves Marty, Wolfgang
- ↑ Numerical Approximation of Rough Invariant Curves of Planar Maps Article in SIAM Journal on Scientific Computing 25(1) · September 2003 DOI: 10.1137/S106482750241373X K. D. Edoh and Jens Lorenz
- ↑ SIAM J. Sci. and Stat. Comput., 8(6), 951–962. (12 pages) A New Algorithm for the Numerical Approximation of an Invariant Curve Published online: 14 July 2006 Keywords invariant manifold, polygonal approximation AMS Subject Headings 65L99, 65H10, 34C40 Publication Data ISSN (print): 0196-5204 ISSN (online): 2168-3417 Publisher: Society for Industrial and Applied Mathematics M. van Veldhuizen
- ↑ Escape lines versus equipotential lines in the Mnadelbrot set by M. Romera, Pastor G , D. de la Guía, Montoya
- ↑ wikipedia : Jordan curve theorem
- ↑ Modeling Julia Sets with Laminations: An Alternative Definition by Debra Mimbs
- ↑ Laminations of the unit disk with irrational rotation gaps by John C. Mayer
- ↑ Rational maps represented by both rabbit and aeroplane matings Thesis submitted in accordance with the requirements of the University of Liverpool for the degree of Doctor in Philosophy by Freddie R. Exall July 2010
- ↑ Rational maps represented by both rabbit and aeroplane matings Thesis submitted in accordance with the requirements of the University of Liverpool for the degree of Doctor in Philosophy by Freddie R. Exall July 2010
- ↑ Iterated Monodromy Groups of Quadratic Polynomials, I Laurent Bartholdi, Volodymyr V. Nekrashevych
- ↑ GROWTH OF GROUPS DEFINED BY AUTOMATA : ASHLEY S. DOUGHERTY, LYDIA R. KINDELIN, AARON M. REAVES, ANDREW J. WALKER, AND NATHANIEL F. ZAKAHI
- ↑ wikipedia : discretization
- ↑ mathinsight : from_discrete_to_continuous_dynamical_systems
- ↑ Symbolic Dynamics of Quadratic Polynomials by H. Bruin and D. Schleicher
- ↑ Symbolic Dynamics and Rotation Numbers J. J. P. Veerman Phys. 13A, 1986, 543-576.
- ↑ Symbolic Dynamics of Order-Preserving Orbits J. J. P. Veerman Phys. 29D, 1987, 191-201.
- ↑ Germ in wikipedia
- ↑ math.stackexchange question : is-there-any-difference-between-mapping-and-function
- ↑ Iterated function (map) in wikipedia
- ↑ evolution function
- ↑ the discrete nonlinear dynamical system
- ↑ A Beginners’ Guide to Resurgence and Trans-series in Quantum Theories Gerald Dunne
- ↑ dinkydauset at deviantar :Perturbation-for-the-Mandelbrot-set-450766847
- ↑ N. Marwan, M. C. Romano, M. Thiel, J. Kurths: Recurrence Plots for the Analysis of Complex Systems, Physics Reports, 438(5-6), 237-329, 2007.
- ↑ math.stackexchange question : definition-of-markov-partition
- ↑ Structure of Inverse Limit Spaces of Tent Maps with Nonrecurrent Critical Points by Brian Raines and Sonja Stimac
- ↑ Bifurcation structures in maps of Henon type by Kai T Hansen and Predrag Cvitanovic
- ↑ Hyperbolic Components by John Milnor
- ↑ Complex quadratic map in wikipedia
- ↑ Michael Yampolsky, Saeed Zakeri : Mating Siegel quadratic polynomials.
- ↑ Mandel: software for real and complex dynamics by Wolf Jung
- ↑ three-cool-facts-about-rotations-of-the-circle by David Richeson
- ↑ irrational-rotations-of-the-circle-and-benfords-law by David Richeson
- ↑ wikipedia : Dyadic transformation
- ↑ lavaurs' algorithm in Haskell with SVG output by Claude Heiland-Allen
- ↑ SYMBOLIC DYNAMICS AND SELF-SIMILAR GROUPS by VOLODYMYR NEKRASHEVYCH
- ↑ The measure of the Feigenbaum Julia set by Artem Dudko and Scott Sutherland
- ↑ Poincaré map
- ↑ General principles of chaotic dynamics by P.B. Persson , C.D. Wagner
- ↑ Continuous time and discrete time dynamical systems by Shaun Bullett
- ↑ Continuous time and discrete time dynamical systems by Shaun Bullett
- ↑ Conformal Geometry and Dynamics of Quadratic Polynomials Mikhail Lyubich
- ↑ binary_shift_left
- ↑ Multiplier at wikipedia
- ↑ wikipedia : Rotation number
- ↑ rotation number From the Mandelbrot Set Glossary and Encyclopedia, by Robert Munafo, (c) 1987-2016
- ↑ scholarpedia : Rotation_theory
- ↑ The Fractal Geometry of the Mandelbrot Set II. How to Count and How to Add Robert L. Devaney
- ↑ An Introduction to Rotation Theory Prize winner, DSWeb Student Competition, 2007 By Christian Kue
- ↑ Complex systems simulation Curso 2012-2013 by Antonio Giraldo and María Asunción Sastre
- ↑ https://plus.maths.org/content/winding-numbers-topography-and-topology-ii
- ↑ wikipedia : orbit (dynamics)
- ↑ Wikipedia : Complex quadratic polynomial - Critical point
- ↑ MandelOrbits - A visual real-time trace of Mandelbrot iterations by Ivan Freyman
- ↑ wikipedia : Periodic points of complex quadratic mappings
- ↑ M. Romera, G. Pastor, and F. Montoya : Multifurcations in nonhyperbolic fixed points of the Mandelbrot map. Fractalia 6, No. 21, 10-12 (1997)
- ↑ Burns A M : Plotting the Escape: An Animation of Parabolic Bifurcations in the Mandelbrot Set. Mathematics Magazine, Vol. 75, No. 2 (Apr., 2002), pp. 104-116
- ↑ Khan Academy : Mandelbrot Spirals 2
- ↑ Complex Power Towers (Or ‘mucking around with Mathematica’) by Mike Croucher
- ↑ /DarkHeart by Chris King
- ↑ Ouadratic-like maps and Renormalization by Nuria Fagella
- ↑ Peiod From the Mandelbrot Set Glossary and Encyclopedia, by Robert Munafo, (c) 1987-2015.
- ↑ scholarpedia : Periodic Orbit for a Map
- ↑ Perturbation for the Mandelbrot set by DinkydauSet, Apr 28, 2014, 3:46:13 PM
- ↑ PARABOLIC IMPLOSION A MINI-COURSE ARNAUD CHERITAT
- ↑ wikipedia : Complex_quadratic_polynomial - Planes
- ↑ Alternate Parameter Planes by David E. Joyce
- ↑ mu-ency : exponential map by R Munafo
- ↑ Exponential mapping and OpenMP by Claude Heiland-Allen
- ↑ Linas Vepstas : Self Similar?
- ↑ the flattened cardioid of a Mandelbrot by Tom Rathborne
- ↑ Stretching cusps by Claude Heiland-Allen
- ↑ Twisted Mandelbrot Sets by Eric C. Hill
- ↑ doubling bifurcations on complex plane by E Demidov
- ↑ On biaccessible points in the Julia set of the family z(a+z^{d}) by Mitsuhiko Imada
- ↑ Surgery in Complex Dynamics by Carsten Lunde Petersen, online paper
- ↑ Nucleus - From the Mandelbrot Set Glossary and Encyclopedia, by Robert Munafo, (c) 1987-2015.
- ↑ Siegel disks by Xavier Buff and Arnaud Ch ́ritat e Univ. Toulouse Roma, April 2009
- ↑ wikipedia : Critical point (mathematics)
- ↑ Java program by Dieter Röß showing result of changing initial point of Mandelbrot iterations
- ↑ Cut point in wikipedia
- ↑ On local connectivity for the Julia set of rational maps : Newton’s famous example By P. Roesch
- ↑ muency : feigenbaum point
- ↑ On Periodic and Chaotic Regions in the Mandelbrot Set by G. Pastor , M. Romera, G. Álvarez, D. Arroyo and F. Montoya
- ↑ fractal-faq : section 6
- ↑ Period doubling and Feigenbaum's scaling be E Demidov
- ↑ mathoverflow question : is-there-a-way-to-find-regions-of-depth-in-the-mandelbrot-set-other-than-simply?rq=1
- ↑ [w:Point at infinity|Point at infinity in wikipedia]
- ↑ Mathoverflow question : Attractive Basins and Loops in Julia Sets
- ↑ wikipedia : Misiurewicz point
- ↑ Symbolic sequences of one-dimensional quadratic map points by G Pastor, Miguel Romera, Fausto Montoya Vitini
- ↑ mathoverflow question : Is there a way to find regions of depth in the Mandelbrot set other than simply poking around?
- ↑ G. Pastor, M. Romera, G. Álvarez, D. Arroyo and F. Montoya, "On periodic and chaotic regions in the Mandelbrot set", Chaos, Solitons & Fractals, 32 (2007) 15-25
- ↑ The bifurcation diagram of cubic polynomial vector fields on CP1 by Christiane Rousseau
- ↑ http://www.mndynamics.com/indexp.html%7C program Mandel by Wolf Jung , demo 2 page 3
- ↑ GROWTH OF GROUPS DEFINED BY AUTOMATA : ASHLEY S. DOUGHERTY, LYDIA R. KINDELIN, AARON M. REAVES, ANDREW J. WALKER, AND NATHANIEL F. ZAKAHI
- ↑ wikipedia : Orbit portrait
- ↑ Airplane primitive parabolic implosion by Wolf Jung
- ↑ CANTOR BOUQUETS, EXPLOSIONS, AND KNASTER CONTINUA: DYNAMICS OF COMPLEX EXPONENTIALS by Robert L. Devaney Publicacions Matematiques, Vol 43 (1999), 27–54.
- ↑ Tuning From the Mandelbrot Set Glossary and Encyclopedia, by Robert Munafo, (c) 1987-2014.
- ↑ wikipedia : Conformal radius
- ↑ scholarpedia : Quadratic Siegel disks
- ↑ Julia Sets of Complex Polynomials and Their Implementation on the Computer by Christoph Martin Stroh
- ↑ fractalforums: bounding circle of julia sets by knighty
- ↑ wikipedia : Sequence
- ↑ wikipedia : series
- ↑ wikipedia : Continuum in set theory
- ↑ Mu-atom From the Mandelbrot Set Glossary and Encyclopedia, by Robert Munafo, (c) 1987-2013.
- ↑ Island Mu-Molecule by Robert P. Munafo, 2012 Aug 18.
- ↑ Internal addresses in the Mandelbrot set and Galois groups of polynomials by Dierk Schleicher, page 31
- ↑ Child From the Mandelbrot Set Glossary and Encyclopedia, by Robert Munafo, (c) 1987-2013.
- ↑ Surgery in Complex Dynamics by Carsten Lunde Petersen, online paper
- ↑ Internal addresses in the Mandelbrot set and irreducibility of polynomials by Dierk Schleicher
- ↑ wikipedia : Carathéodory's theorem (conformal mapping)
- ↑ The intrinsic geometry of a Jordan domain by Richard L. Bishop
- ↑ fractalforums : binary-decomposition-and-external-angles by Claude
- ↑ Norman Lebovitz : Textbook for Mathematics 27300
- ↑ wikipedia : Level set
- ↑ A. Blokh, X. Buff, A. Cheritat, L. Oversteegen The solar Julia sets of basic quadratic Cremer polynomials, Ergodic Theory and Dynamical Systems , 30 (2010), #1, 51-65
- ↑ wikipedioa: Surgery theory
- ↑ Fractus doc by Richard Rosenman
- ↑ wikipedia : Escaping set
- ↑ fractint doc : bailout
- ↑ Dessins d’enfants and Hubbard trees by Kevin M. Pilgrim