Fractals/Iterations in the complex plane/Mandelbrot set

< Fractals < Iterations in the complex plane

This book shows how to code different algorithms for drawing parameter plane ^[1] ( Mandelbrot set ^[2] ) for complex quadratic polynomial ^[3].

One can find different types of points / sets on parameter plane ^[4]

Exterior of Mandelbrot set

Extrerior

Boundary of Mandelbrot set

description

Interior of Mandelbrot set - hyperbolic components

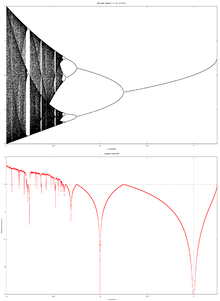
The Lyapunov Exponent

Lyapunov exponents of mini the Mandelbrot set

Lyapunov exponent of real quadratic map

Math equation :^[5]

$\lambda _{f}(z_{0})=\lim _{n\rightarrow \infty }{\frac {1}{n}}\sum _{i=0}^{n-1}\left(\ln \left|f'(z_{i})\right|\right)$

where :

$f'(x)={\frac {d}{dz}}f_{c}(z)=2z$

means first derivative of f with respect to z

Interior distance estimation

Interior distance estimation

Description of method

absolute value of the orbit

# Hypercomputing the Mandelbrot Set? by Petrus H. Potgieter February 1, 2008
n=1000; # For an nxn grid
m=50; # Number of iterations
c=meshgrid(linspace(-2,2,n))\ # Set up grid
+i*meshgrid(linspace(2,-2,n))’;
x=zeros(n,n); # Initial value on grid
for i=1:m
x=x.^2+c; # Iterate the mapping
endfor
imagesc(min(abs(x),2.1)) # Plot monochrome, absolute
# value of 2.1 is escape

internal level sets

Color of point :

is proportional to the value of z is at final iteration.
shows internal level sets of periodic attractors.

bof60

Image of bof60 in on page 60 in the book "the Beauty Of Fractals".Description of the method described on page 63 of bof. It is used only for interior points of the Mandelbrot set.

Color of point is proportional to :

the smallest distance of its orbit from origin^[8]^[9]
the smallest value z gets during iteration ^[10]
illuminating the closest approach the iterates of the origin (critical point) make to the origin inside the set
"Each pixel of each particular video frame represents a particular complex number c = a + ib. For each sequential frame n, the magnitude of z(c,n) := z(c, n-1)^2 + c is displayed as a grayscale intensity value at each of these points c: larger magnitude points are whiter, smaller magnitudes are darker. As n rises from 1 to 256, points outside the Mandelbrot Set quickly saturate to pure white, while points within the Mandelbrot Set oscillate through the darker intensities." Brian Gawalt ^[11]

Level sets of distance are sets of points with the same distance^[12]

if (Iteration==IterationMax)
 /* interior of Mandelbrot set = color is proportional to modulus of last iteration */
 else { /* exterior of Mandelbrot set = black */
  color[0]=0;
  color[1]=0;
  color[2]=0;                           
 }

fragment of code : fractint.cfrm from Gnofract4d ^[13]

bof60 {
 init:
       float mag_of_closest_point = 1e100
 loop:
       float zmag = |z|
       if zmag < mag_of_closest_point
               mag_of_closest_point = zmag
       endif
 final:
       #index = sqrt(mag_of_closest_point) * 75.0/256.0
}

bof61

Names and description

period domain
atom domain
BOF61
orbit trap at (0,0)

Period of hyperbolic components

period of hyperbolic components

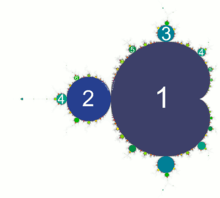
Period of hyperbolic component of Mandelbrot set is a period of limit set of critical orbit.

Algorithms for computing period:

direct period detection from iterations of critical point z = 0.0 on dynamical plane
"quick and dirty" algorithm : check if $abs(z_{n})<eps$ then colour c-point with colour n. Here n is a period of attracting orbit and eps is a radius of circle around attracting point = precision of numerical computations
"methods based on interval arithmetic when implemented properly are capable of finding all period-n cycles for considerable large n." (ZBIGNIEW GALIAS )^[14]
Floyd's cycle-finding algorithm ^[15]
the spider algorithm
atom domain, BOF61

Multiplier map

definition

interior coordinate ^[16]^[17]

Fractint

Fractint : Color Parameters : INSIDE=ATAN

colors by determining the angle in degrees the last iterated value has with respect to the real axis, and using the absolute value. This feature should be used with periodicity=0^[18]

Internal angle

Method by Renato Fonseca : ^[19] "a point c in the set is given a hue equal to argument

$arg(z_{n_{max}})=arctan{\frac {Im(z_{n_{max}})}{Re(z_{n_{max}})}}$

(scaled appropriatly so that we end up with a number in the range 0 - 255). The number z_nmax is the last one calculated in the z's sequence. "

Internal rays

Internal and external rays

When $radius\,$ varies and $angle\,$ is constant then $c\,$ goes along internal ray. It is used as a path inside Mandelbrot set

/* find c in component of Mandelbrot set 
 uses complex type so #include <complex.h> and -lm 
 uses code by Wolf Jung from program Mandel
 see function mndlbrot::bifurcate from mandelbrot.cpp
 http://www.mndynamics.com/indexp.html

  */
double complex GiveC(double InternalAngleInTurns, double InternalRadius, unsigned int period)
{
  //0 <= InternalRay<= 1
  //0 <= InternalAngleInTurns <=1
  double t = InternalAngleInTurns *2*M_PI; // from turns to radians
  double R2 = InternalRadius * InternalRadius;
  double Cx, Cy; /* C = Cx+Cy*i */
  switch ( period ) {
    case 1: // main cardioid
      Cx = (cos(t)*InternalRadius)/2-(cos(2*t)*R2)/4; 
      Cy = (sin(t)*InternalRadius)/2-(sin(2*t)*R2)/4; 
      break;
   case 2: // only one component 
      Cx = InternalRadius * 0.25*cos(t) - 1.0;
      Cy = InternalRadius * 0.25*sin(t); 
      break;
  // for each period  there are 2^(period-1) roots. 
  default: // safe values
      Cx = 0.0;
      Cy = 0.0; 
    break; }

  return Cx+ Cy*I;
}

// draws points to memmory array data
int DrawInternalRay(double InternalAngleInTurns , unsigned int period, int iMax, unsigned char data[])
{

   complex double c;
   double InternalRadius;
   double RadiusStep; // between radius of points 
   int i; // number of point to draw
      
  RadiusStep = 1.0/iMax;
   
  for(i=0;i<=iMax;++i){ 
   InternalRadius = i * RadiusStep;
   c = GiveC(InternalAngleInTurns, InternalRadius, period);
   DrawPoint(c,data);
  }

return 0;
}

Example : internal ray of angle =1/6 of main cardioid.

Internal angle :

$angle=1/6\,$

radius of ray :

$0\leq radius\leq 1\,$

Point of internal radius of unit circle :

$w=radius*e^{i*angle}\,$

Map point $w$ to parameter plane :

$c={\frac {w}{2}}-{\frac {w^{2}}{4}}\,$

For $epsilon=0\,$ this is equation for main cardioid.

Internal curve

When $radius\,$ is constant varies and $angle\,$ varies then $c\,$ goes along internal curve.

/* find c in component of Mandelbrot set 
 uses complex type so #include <complex.h> and -lm 
 uses code by Wolf Jung from program Mandel
 see function mndlbrot::bifurcate from mandelbrot.cpp
 http://www.mndynamics.com/indexp.html

  */
double complex GiveC(double InternalAngleInTurns, double InternalRadius, unsigned int period)
{
  //0 <= InternalRay<= 1
  //0 <= InternalAngleInTurns <=1
  double t = InternalAngleInTurns *2*M_PI; // from turns to radians
  double R2 = InternalRadius * InternalRadius;
  double Cx, Cy; /* C = Cx+Cy*i */
  switch ( period ) {
    case 1: // main cardioid
      Cx = (cos(t)*InternalRadius)/2-(cos(2*t)*R2)/4; 
      Cy = (sin(t)*InternalRadius)/2-(sin(2*t)*R2)/4; 
      break;
   case 2: // only one component 
      Cx = InternalRadius * 0.25*cos(t) - 1.0;
      Cy = InternalRadius * 0.25*sin(t); 
      break;
  // for each period  there are 2^(period-1) roots. 
  default: // safe values
      Cx = 0.0;
      Cy = 0.0; 
    break; }

  return Cx+ Cy*I;
}


// draws points to memmory array data
int DrawInternalCurve(double InternalRadius , unsigned int period,  int iMax, unsigned char data[])
{

   complex double c;
   double InternalAngle; // in turns = from 0.0 to 1.0
   double AngleStep;
   int i;
   // int iMax =100;
   
  AngleStep = 1.0/iMax;
   
  for(i=0;i<=iMax;++i){ 
   InternalAngle = i * AngleStep;
   c = GiveC(InternalAngle, InternalRadius, period);
   DrawPoint(c,data);
  }

return 0;
}

Boundaries of hyperbolic components

description

Centers of components

Video

see 3D

Speed improvements - optimisation

Symmetry

The Mandelbrot set is symmetric with respect to the x-axis in the plane :

colour(x,y) = colour(x,-y)

its intersection with the x-axis ( real slice of Mandelbrot set ) is an interval :

<-2 ; 1/4>

It can be used to speed up computations ( up to 2-times )^[20]

Bailout test

Instead of checking :

 ${\sqrt {Z_{x}^{2}+Z_{y}^{2}}}<ER$

compute ER2 once and check :

 $Z_{x}^{2}+Z_{y}^{2}<ER^{2}$

It gives the same result and is faster.

Period detection

"When rendering a Mandelbrot or Julia set, the most time-consuming parts of the image are the “black areas”. In these areas, the iterations never escape to infinity, so every pixel must be iterated to the maximum limit. Therefore, much time can be saved by using an algorithm to detect these areas in advance, so that they can be immediately coloured black, rather than rendering them in the normal way, pixel by pixel. FractalNet uses a recursive algorithm to split the image up into blocks, and tests each block to see whether it lies inside a “black area”. In this way, large areas of the image can be quickly coloured black, often saving a lot of rendering time. ... (some) blocks were detected as “black areas” and coloured black immediately, without having to be rendered. (Other) blocks were rendered in the normal way, pixel by pixel." Michael Hogg ^[21]

 // cpp code by Geek3 
// http://commons.wikimedia.org/wiki/File:Mandelbrot_set_rainbow_colors.png
bool outcircle(double center_x, double center_y, double r, double x, double y)
{ // checks if (x,y) is outside the circle around (center_x,center_y) with radius r
        x -= center_x;
        y -= center_y;
        if (x * x + y * y > r * r)
                return(true);
        return(false);

 // skip values we know they are inside
                        if ((outcircle(-0.11, 0.0, 0.63, x0, y0) || x0 > 0.1)
                                && outcircle(-1.0, 0.0, 0.25, x0, y0)
                                && outcircle(-0.125, 0.744, 0.092, x0, y0)
                                && outcircle(-1.308, 0.0, 0.058, x0, y0)
                                && outcircle(0.0, 0.25, 0.35, x0, y0))
                        {
                          // code for iteration
                         }

Cardioid and period-2 checking

One way to improve calculations is to find out beforehand whether the given point lies within the cardioid or in the period-2 bulb. Before passing the complex value through the escape time algorithm, first check if:

(x+1)^{2}+y^{2}<{\frac {1}{16}}

to determine if the point lies within the period-2 bulb and

q=\left(x-{\frac {1}{4}}\right)^{2}+y^{2}

q\left(q+\left(x-{\frac {1}{4}}\right)\right)<{\frac {1}{4}}y^{2}.

to determine if the point lies inside the main cardioid.

Periodicity checking

Most points inside the Mandelbrot set oscillate within a fixed orbit. There could be anything from ten to tens of thousands of points in between, but if an orbit ever reaches a point where it has been before then it will continually follow this path, will never tend towards infinity and hence is in the Mandelbrot set. This Mandelbrot processor includes periodicity checking (and p-2 bulb/cardioid checking) for a great speed up during deep zoom animations with a high maximum iteration value.

Perturbation theory

Description

Very highly magnified images require more than the standard 64-128 or so bits of precision most hardware floating-point units provide, requiring renderers use slow "bignum" or "arbitrary precision"^[22] math libraries to calculate. However, this can be sped up by the exploitation of perturbation theory^[23]. Given

z_{n+1}=z_{n}^{2}+c

as the iteration, and a small epsilon, it is the case that

(z_{n}+\epsilon )^{2}+c=z_{n}^{2}+2z_{n}\epsilon +\epsilon ^{2}+c

z_{n+1}+2z_{n}\epsilon +\epsilon ^{2}

so if one defines

\epsilon _{n+1}=2z_{n}\epsilon _{n}+\epsilon _{n}^{2}

one can calculate a single point (e.g. the center of an image) using normal, high-precision arithmetic (z), giving a reference orbit, and then compute many points around it in terms of various initial offsets epsilon-zero plus the above iteration for epsilon. For most iterations, epsilon does not need more than 16 significant figures, and consequently hardware floating-point may be used to get a mostly accurate image.^[24] There will often be some areas where the orbits of points diverge enough from the reference orbit that extra precision is needed on those points, or else additional local high-precision-calculated reference orbits are needed. This rendering method, and particularly the automated detection of the need for additional reference orbits and automated optimal selection of same, is an area of ongoing, active research. Renderers implementing the technique are publicly available and offer speedups for highly magnified images in the multiple orders of magnitude range.^[25] ^[26] ^[27]

Newton-Raphson zooming

One can "use newton's method to find and progressively refine the precision of the location of the minibrot at the center of a pattern. This allows them to arbitrarily select a magnification between the location they started at and the final minibrot they calculate to be at the center of that location."^[28]^[29]

Glitches

Glitches^[30]

history

2 independent descriptions :
- Fast Mandelbrot set with infinite resolution by Sergey Khashin (July 9, 2011)^[31]
- perturbation method by K.I. Martin (2013-05-18)^[32]
extending Martin's description to handle interior distance estimation too by Claude Heiland-Allen^[33]

Programs

SuperFractalThing in Java by K.I. Martin^[34]
mightymandel by Claude Heiland-Allen^[35]
mandelbrot-perturbator by Claude Heiland-Allen : http://code.mathr.co.uk/mandelbrot-perturbator/
Kalles Fraktaler for windows

References

Notes

^ It is conjectured that the polynomials (for the centers) are irreducible, but this has not been proved yet - Wolf Jung

This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

Fractals/Iterations in the complex plane/Mandelbrot set

Exterior of Mandelbrot set

Boundary of Mandelbrot set

Interior of Mandelbrot set - hyperbolic components

The Lyapunov Exponent

Interior distance estimation

absolute value of the orbit

internal level sets

bof60

bof61

Period of hyperbolic components

Multiplier map

Fractint

Internal angle

Internal rays

Internal curve

Boundaries of hyperbolic components

Centers of components

Video

Speed improvements - optimisation

Symmetry

Bailout test

Period detection

Cardioid and period-2 checking

Periodicity checking

Perturbation theory

Description

Newton-Raphson zooming

Glitches

history

Programs

More tutorials and code

References

Notes