Fractals/Iterations in the complex plane/Fatou set
< Fractals < Iterations in the complex planeFatou components
In case of discrete dynamical system based on complex quadratic polynomial Fatou set can consist of components :
- attarcting ( basin of attraction of fixed point / cycle )
- superattracting ( Boettcher coordinate )
- attracting but not superattracting (
- parabolic (Leau-Fatou) basin ( Fatou coordinate ) Local dynamics near rationally indifferent fixed point/cycle ;
- elliptic basin = Siegel disc ( Local dynamics near irrationally indifferent fixed point/cycle )
Local discrete dynamics
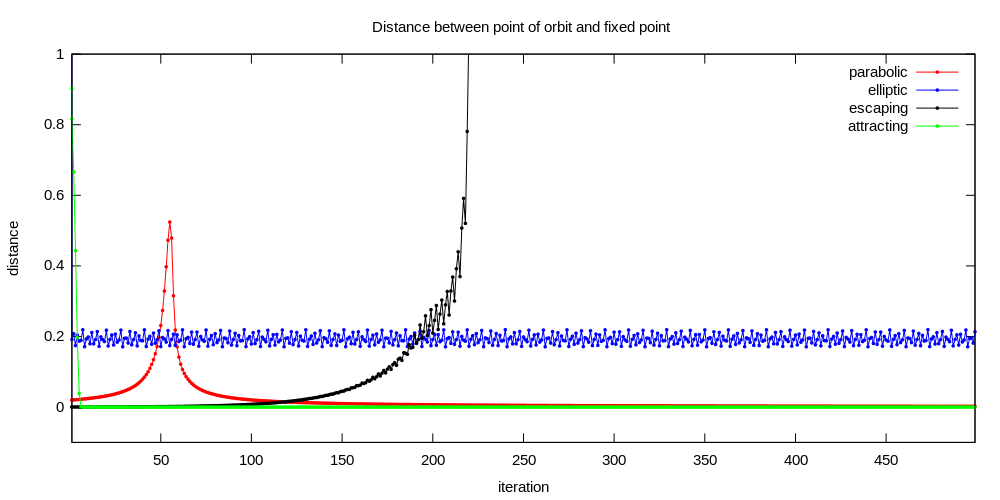
Types of dynamics
- attracting : hyperbolic dynamics
- superattracting : the very fast ( = exponential) convergence to periodic cycle ( fixed point )
- parabolic component = slow ( lazy ) dynamics = slow ( exponential slowdown) convergence to parabolic fixed point ( periodic cycle)
- Siegel disc component = rotation around fixed point and never reach the fixed point
Tests
Analysis of local dynamics :
- drawing critical orbit(s)
- finding periodic points
- dividing complex move into simple paths
- topological graph, [1]
- drawing grid ( polar or rectangular )
| method | test | description | resulting sets | true sets | |
|---|---|---|---|---|---|
| binary escape time | bailout | abs(zn)>ER | escaping and not escaping | Escaping set contains fast escaping pixels and is a true exterior.
Not escaping set is treated as a filled Julia set ( interior and boundary) but it contains :
| |
| discrete escape time = Level Set Method = LSM | bailout | Last iteration or final_n = n : abs(zn)>ER | escaping set is divided into subsets with the same n ( last iteration). This subsets are called Level Sets and create bands surrounding and approximating Julia set. Boundaries of level sets are called dwell-bands | ||
| continous escape time | Example | Example | Example |
References
- ↑ A Topology Simplification Method For 2D Vector Fields by Xavier Tricoche, Gerik Scheuermann and Hans Hagen
This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.