Fractals/Computer graphic techniques/2D/plane

< Fractals < Computer graphic techniques < 2D

Coordinate

There are different 2D coordinate systems :[1]

Viewport = part of the plane

A viewport is a polygon viewing region in computer graphics.[2]

Types

Relation between these 2 types creates new items :

parameter files

Parameters can be read from both parameter and image files :[5]

Reading parameters

/*
  from  gui main.c
  https://gitorious.org/maximus/book/source/47ce485c4266b3d5fc62f685f001ce7606ce426f:
  by 
  http://mathr.co.uk/blog/   

  loads txt file with parameters
  http://qualapps.blogspot.com/2009/01/unicode-bom-handling-in-c-run-time.html
  http://www.joelonsoftware.com/articles/Unicode.html
  http://programmers.stackexchange.com/questions/102205/should-utf-16-be-considered-harmful
  http://utf8everywhere.org/
  http://www.codeguru.com/cpp/misc/misc/multi-lingualsupport/article.php/c10451/The-Basics-of-UTF8.htm
  http://stackoverflow.com/questions/2113270/how-to-read-unicode-utf-8-binary-file-line-by-line
  http://www.cl.cam.ac.uk/~mgk25/unicode.html

  gcc l.c -lmpfr -lgmp -Wall


*/
#include <stdio.h>
#include <stdlib.h> // malloc
#include <string.h> // strncmp
#include <ctype.h> // isascii
#include <mpfr.h>



struct view {
  mpfr_t cx, cy, radius, pixel_spacing;
};

static struct view *view_new() {
  struct view *v = malloc(sizeof(struct view));
  mpfr_init2(v->cx, 53);
  mpfr_init2(v->cy, 53);
  mpfr_init2(v->radius, 53);
  mpfr_init2(v->pixel_spacing, 53);
  return v;
}

static void view_delete(struct view *v) {
  mpfr_clear(v->cx);
  mpfr_clear(v->cy);
  mpfr_clear(v->radius);
  mpfr_clear(v->pixel_spacing);
  free(v);
}


//http://stackoverflow.com/questions/5457608/how-to-remove-a-character-from-a-string-in-c?rq=1
// Fabio Cabral
void removeChar(char *str, char garbage) {

    char *src, *dst;
    for (src = dst = str; *src != '\0'; src++) {
        *dst = *src;
        if (*dst != garbage) dst++;
    }
    *dst = '\0';
}

// https://en.wikipedia.org/wiki/Serialization
// read data from file 
static int deserialize(const char *filename) {

  // open file in a text mode 
  FILE *in = fopen(filename, "r");

  if (in) {
    printf( "file %s opened\n", filename);
    char *line = 0;
    size_t linelen = 0;
    ssize_t readlen = 0; // bytes_read = length of the line 
    
    // read line 
    while (-1 != (readlen = getline(&line, &linelen, in)))     
      {
        // 
	if (readlen && line[readlen-1] == '\n') { 
	  line[readlen - 1] = 0; }

	// remove BOM 
        while  (! isascii(line[0])) 
               {printf(" removed non-printing char = %c ( non -ASCII char ) = %3d  (signed 8 bit) = %u (unsigned 8 bit) =  0x%.2X (hexadecimal) \n", line[0], line[0], (unsigned char) line[0], (unsigned char) line[0]);
                removeChar(line,line[0]);
                }
                
       
	// size 
	if (0 == strncmp(line, "size ", 5)) 
	  {

	    printf( "size line found :");
    
	    int w = 0, h = 0;
	    sscanf(line + 5, "%d %d\n", &w, &h);
	    printf( "size of image in pixels : width = %d   ; height = %d \n", w,h);
	    // resize_image(w, h); // FIXME TODO make this work...
	  } 
         
        //  view
        else if (0 == strncmp(line, "view ", 5)) 
	  {
	    printf( "view line found : \n");
	    int p = 53;
	    char *xs = malloc(readlen);   
	    char *ys = malloc(readlen);
	    char *rs = malloc(readlen);
	    sscanf(line + 5, "%d %s %s %s", &p, xs, ys, rs);

	    struct view *v = view_new();
	    mpfr_set_prec(v->cx, p);
	    mpfr_set_prec(v->cy, p);
	    mpfr_set_str(v->cx, xs, 0, GMP_RNDN);
	    mpfr_set_str(v->cy, ys, 0, GMP_RNDN);
	    mpfr_set_str(v->radius, rs, 0, GMP_RNDN);
	    //
	    printf ("precision p  =  %d\n", p);
	    printf ("center =  ");
	    mpfr_out_str (stdout, 10, p, v->cx, MPFR_RNDD);
	    printf (" ; ");
	    mpfr_out_str (stdout, 10, p, v->cy, MPFR_RNDD);
	    putchar ('\n');  

	    printf ("radius =  ");
	    mpfr_out_str (stdout, 10, p, v->radius, MPFR_RNDD);
	    putchar ('\n');  


	    free(xs);
	    free(ys);
	    free(rs);
	    view_delete(v);
        
	  } 
         
	else if (0 == strncmp(line, "ray_out ", 8)) 
	  {
	    printf( "ray_out line found :\n");
	    int p = 53;
	    char *xs = malloc(readlen);
	    char *ys = malloc(readlen);
	    sscanf(line + 8, "%d %s %s", &p, xs, ys);
	    mpfr_t cx, cy;
	    mpfr_init2(cx, p);
	    mpfr_init2(cy, p);
	    mpfr_set_str(cx, xs, 0, GMP_RNDN);
	    mpfr_set_str(cy, ys, 0, GMP_RNDN);
	    free(xs);
	    free(ys);
           
	    mpfr_clear(cx);
	    mpfr_clear(cy);
	  } 
        
        else if (0 == strncmp(line, "ray_in ", 7)) {
	  printf( "ray_in line found : \n");
	  int depth = 1000;
	  char *as = malloc(readlen);
	  sscanf(line + 7, "%d %s", &depth, as);
        
	  free(as);
	} 
      
	else if (0 == strncmp(line, "text ", 20)) {
	  printf( "text line found : \n");
	  //int p = 53;
	  char *xs= malloc(readlen);
	  char *ys = malloc(readlen);
	  char *ss = malloc(readlen);
	  sscanf(line + 20, "%s %s %s \n", xs, ys, ss);
        
       
	  free(xs);
	  free(ys);
	  free(ss);
	}

      
	else if (0 == strncmp(line, "//", 2 )) {
	  printf( "line of comment found : %s\n", line );
        
        }
	else printf( "not-known line found ! Maybe line with BOM ? \n");


      } // while 

    free(line);
    fclose(in);
    printf( "file %s closed\n", filename);
    return 0;} 
 
  // if (in)
  else {
    printf( "file %s not opened = error !\n", filename);  
    return 1;}
}


int main (int argc, const char* argv[]) 
{

  if (argc != 2) {
    fprintf(stderr, "program opens text file \n");
    fprintf(stderr, "program input : text file with parameters \n");
    fprintf(stderr, "usage: %s filename\n", argv[0]);
    return 1;
  }

  deserialize(argv[1]);


  return 0;
}

Description

Rectangle part of 2D plane can be described by :

"People specify fractal coordinates in many ways. Some people use the coordinates of the upper-left and lower-right visible points, specifying the coordinates as four numbers x1, y1, x2, y2. To set the same viewpoint in XaoS, set the real portion of the center to (x1+x2)/2, the imaginary part of center to (y1+y2)/2, and the radius to the greater of x2-x1 and y2-y1." ( from Xaos doc[6] )

Corners

Standard description in Fractint, Ultra Fractal, ChaosPro and Fractal Explorer are corners. For example initial plane for Mandelbrot set is 

 Corners:                X                     Y
 Top-l          -2.5000000000000000    1.5000000000000000
 Bot-r           1.5000000000000000   -1.5000000000000000
 Ctr -0.5000000000000000   0.0000000000000000  Mag 6.66666667e-01
 X-Mag-Factor     1.0000   Rotation    0.000   Skew    0.000

Display window of parameter plane has :


See demo par file :

Mandel_Demo        { ; PAR for initialization of Fractint demo
  reset=1900 type=mandel corners=-2.5/1.5/-1.5/1.5 params=0/0 inside=0
  sound=no
  }

For julia set/ dynamic plane has : 

Corners:                X                     Y
Top-l          -2.0000000000000000    1.5000000000000000
Bot-r           2.0000000000000000   -1.5000000000000000
Ctr  0.0000000000000000   0.0000000000000000  Mag 6.66666667e-01
X-Mag-Factor     1.0000   Rotation    0.000   Skew    0.000


Description from documentation of Fractint :


CORNERS=[xmin/xmax/ymin/ymax[/x3rd/y3rd]]

Example: corners=-0.739/-0.736/0.288/0.291

Begin with these coordinates as the range of x and y coordinates, rather than the default values of (for type=mandel) -2.0/2.0/-1.5/1.5. When you specify four values (the usual case), this defines a rectangle: x- coordinates are mapped to the screen, left to right, from xmin to xmax, y-coordinates are mapped to the screen, bottom to top, from ymin to ymax. Six parameters can be used to describe any rotated or stretched parallelogram: (xmin,ymax) are the coordinates used for the top-left corner of the screen, (xmax,ymin) for the bottom-right corner, and (x3rd,y3rd) for the bottom-left. Entering just "CORNERS=" tells Fractint to use this form (the default mode) rather than CENTER-MAG (see below) when saving parameters with the [B] command.

Center and ...

magnification

CENTER-MAG=[Xctr/Yctr/Mag[/Xmagfactor/Rotation/Skew]]

This is an alternative way to enter corners as a center point and a magnification that is popular with some fractal programs and publications. Entering just "CENTER-MAG=" tells Fractint to use this form rather than CORNERS (see above) when saving parameters with the [B] command. The [TAB] status display shows the "corners" in both forms. When you specify three values (the usual case), this defines a rectangle: (Xctr, Yctr) specifies the coordinates of the center of the image.

Mag indicates the amount of magnification to use. Initial value ( no zoom ) is 6.66666667e-01.

Six parameters can be used to describe any rotated or stretched parallelogram: Xmagfactor tells how many times bigger the x- magnification is than the y-magnification,

Rotation indicates how many degrees the image has been turned.

Skew tells how many degrees the image is leaning over. Positive angles will rotate and skew the image counter-clockwise.


Parameters can be saved to parmfile called fractint.par

width

Wolf Jung uses center and width in Mandel: 

/* 
   from mndlbrot.cpp  by Wolf Jung (C) 201
   These classes are part of Mandel 5.7, which is free software; you can
   redistribute and / or modify them under the terms of the GNU General
   Public License as published by the Free Software Foundation; either
   version 3, or (at your option) any later version. In short: there is
   no warranty of any kind; you must redistribute the source code as well
*/
void mndlbrot::startPlane(int sg, double &xmid, double &rewidth) const
{  if (sg > 0) 
     { xmid = -0.5; rewidth = 1.6; } // parameter plane
     else { xmid = 0; rewidth = 2.0; } // dynamic plane

width and height

to describe plane ( view ) Xaos uses:

Xaos uses to call it "radius" but it is defind as : the greater of (x2-x1= width) and y2-y1=height."

radius

Claude Heiland-Allen[7] use center and radius for parameter plane of complex quadratic polynomial:

Radius is defined as "the difference in imaginary coordinate between the center and the top of the axis-aligned view rectangle". 

view="-0.75 0 1.5" # standard view of parameter plane : center_re, center_im, radius


  // modified code using center and radius to scan the plane 
  int height = 720;
  int width = 1280;
  double dWidth;
  double dRadius = 1.5;
  double complex center= -0.75*I;
  double complex c;
  int i,j;

  double width2; // = width/2.0
  double height2; // = height/2.0
  
  width2 = width /2.0;
  height2 = height/2.0;

complex double coordinate(int i, int j, int width, int height, complex double center, double radius) {
  double x = (i - width /2.0) / (height/2.0);
  double y = (j - height/2.0) / (height/2.0);
  complex double c = center + radius * (x - I * y);
  return c;
}

for ( j = 0; j < height; ++j) {
    for ( i = 0; i < width; ++i) {
      c = coordinate(i, j, width, height, center, dRadius);
      // do smth 
       }
     }

The same in GLSL ( for Shadertoy) :

 
vec2 GiveCoordinate(vec2 center, float radius, vec2 fragCoord, vec3 iResolution)
{
 
  // from pixel to world coordinate   
  // now point (0,0) is left bottom
  // point (iResolution.x, iResolution.y) is right top   
  float x = (fragCoord.x -  iResolution.x/2.0)/ (iResolution.y/2.0);
  float y = (fragCoord.y -  iResolution.y/2.0)/ (iResolution.y/2.0);
  vec2 c = vec2(center.x + radius*x, center.y + radius*y) ;  
  return c ; 
}

Orientation

Check orientation of the plane by marking first quadrant of Cartesian plane : 

if (x>0 && y>0) Color=MaxColor-Color;

It should be in upper right position.

Optimisation

Scanning

See :

All the pixels

Scan the plane :


Here in Lisp

; common lisp. Here float values can be used,  there is no mapping
(loop for y from -1.5 to 1.5 by 0.1 do
      (loop for x from -2.5 to 0.5 by 0.05 do
            (princ (code-char 42))) ; print char
      (format t "~%")) ; new line

and in C

/* c */
/* screen coordinate = coordinate of pixels */      
int iX, iY, 
iXmin=0, iXmax=1000,
iYmin=0, iYmax=1000,
iWidth=iXmax-iXmin+1,
iHeight=iYmax-iYmin+1;

/* world ( double) coordinate = parameter plane*/
const double ZxMin=-5;
const double ZxMax=5;
const double ZyMin=-5;
const double ZyMax=5;

/* */
double PixelWidth=(ZxMax-ZxMin)/iWidth;
double PixelHeight=(ZyMax-ZyMin)/iHeight;
double Zx, Zy,    /* Z=Zx+Zy*i   */
       Z0x, Z0y,  /* Z0 = Z0x + Z0y*i */

 for(iY=0;iY<iYmax;++iY)
      { Z0y=ZyMin + iY*PixelHeight; /* mapping from screen to world; reverse Y  axis */
        if (fabs(Z0y)<PixelHeight/2) Z0y=0.0; /* Zy = 0 is a special value  */    
        for(iX=0;iX<iXmax;++iX)
         {    /* initial value of orbit Z0 */
           Z0x=ZxMin + iX*PixelWidth;
          }
      }

Plane transformations

Conformal map

Conformal map

cylindrical projection

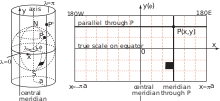
The geometry for the normal (equatorial) tangent projections of the sphere to the cylinder.

Cylindrical projection ( or cylindric p. ) maps from sphere ( without poles) to cylinder [19][20]

Joukowsky transformation (map)

Description :

Mercator map

"the exponential map[22] (aka log polar or mercator projection)" [23]


" it is a log map toward the target point (or, as some might say, a Mercator projection with the target point as South pole and complex ∞ as North pole); horizontally it is periodic and I have placed two periods side to side, whereas vertically it extends to infinity at the top and at the bottom, which corresponds to zooming infinitely far out or in, at a factor of exp(2π)≈535.5 for every size of a horizontal period. Horizontal lines (“parallels”) on the log map correspond to concentric circles around the target point, and vertical lines to radii emanating from it; and the anamorphosis preserves angles." David Madore [24]

" The idea is to focus on a point in or near the Mandelbrot set, and create an image where one direction is the logarithm of the distance and the other one the angle. The result is very much like the astro-ph/031571 map[25] and theXKCD cartoon versions[26]. This map projection is conformal, so it does not distort local angles, and objects are usually recognizable on all scales." Anders Sandberg[27]

Exponential map by R Munafo [28]

Zoom

Mandelbrot zoom created using Double-double precision

Zoom can be used for making :


Notation

If you want to zoom [29]

baseSize // constant value =  extend in real and imaginary axis when zoomLevel is zero.
zoomLevel // inital value = 0.0
zoomFactor = 2^(-zoomLevel) // initial value = 1.0 = no zoom
sizeX = zoomFactor * baseSize
sizeY = zoomFactor * baseSize   
minImaginary = centerY - sizeY/2
maxImaginary = centerY + sizeY/2

Note that base of zoom factor is important when one wants to optimize zooming by using previosly computed pixels.


Usually other notation is used :

baseSize // constant value =  extend in real and imaginary axis when zoomLevel is zero.
zoomLevel // inital value = 0.0
zoomFactor = 10^zoomLevel // initial value = 1.0 = no zoom
sizeX =  baseSize / zoomFactor
sizeY = baseSize / zoomFactor   
minImaginary = centerY - sizeY/2
maxImaginary = centerY + sizeY/2


" Some programs use a power of 2, others use scientific notation. " Dinkydau[30]

magnification = 2^(6901.591) = 3.8539742140068607747447368372813E2077 = 3.8539742140068607747447368372813 *10^(2077)

Pixel size

Pixel size ( = pixel spacing ) is size of a pixel in a world coordinate. For linear scale and same resolution on both axes : 

iSize = iXmax - iXmin ; // width of image in pixels ( integer or screen ) coordinate ; pixels are numbered from iXmin to iXmax; image is rectangular
fSize = CxMax-CxMin // width of image in world ( floating point ) coordinate
PixelWidth = fWidth / iWidth
PixelSize = PixelWidth //
n = Zoom exponent mag = Zoom level [31] Image size in pixels = iSize Image size = fSize PixelSize Decimal digits Binary digits ( precision) radius=fSize/2 = 1/mag
0.666666667 1.0e.666666667 1000 3 0.003 1.5
0 1 = 10^0 = 1.0e0 1000 2.0 0.002 1.0
1 10 = 10^1 =1.0e1 1000 0.2 0.0002 0.1
2 100 = 10^2 = 1.0e2 1000 0.02 0.00002 6 0.01
3 1000 = 10^3 = 1.0e3 1000 0.002 0.00000027 0.001
275 2.1*10^{275} = 2.1E275[32] 1000 1.42857142857143*10^{−275} 1.42857142857143*10^{−278} 278945
2167 1E2167 [33]
n 10^n iSize fSize fSize/iSizen+3 3.4*(n+3) 1/10^n

See also

Maximal zoom

Maximal zoom factor is :[34]fractalforums : world-record-list-for-deepest-mandelbrot-set-zooms


Maximal zoom is correlated with :

Examples :

Optimisation

Precision

What precision do I need for zoom ?[46]

/*
  gcc -Wall  p.c -lm 
  ./a.out

What precision do I need for zoom ?



based on the code from :
 git clone http://code.mathr.co.uk/book.git
unnamed c program by Claude Heiland-Allen


*/


#include <stdio.h>
#include <stdlib.h>
#include <math.h> // log2l





int PrintInfo(int pixel_spacing_bits)
{
  
  if (pixel_spacing_bits <= 40) { printf("use float \n"); return 0;}
  if (pixel_spacing_bits > 60)  
      {printf("use arbitrary precision number, like MPFR \n");
      return 0; }
  
  if (pixel_spacing_bits > 50)   
       {printf("use long double \n");
        return 0; }

  if (pixel_spacing_bits > 40)  
       printf("use double \n");
  
 return 0;
}





int main() {
  
  // int iWidth = 1000;
  int iHeight = 1000;
  long double lRadius = 1.5;
  long double lPixelSpacing ; // = pixel size 
  int iPixelSpacingBits ;  // precision in binary digits or bits 
  long double lMagnification;
  int i;



  

  
  for ( i = 1; i < 100; ++i)
  {

  lMagnification = 1.0/lRadius; 
  lPixelSpacing = lRadius / (iHeight / 2.0); // = pixel size 
  iPixelSpacingBits = -log2l( lPixelSpacing); // 
  printf("Magnification = %12Le ; radius = %12Le ; PixelSpacing = %12Le ; PixelSpacingBits = %d ", lMagnification, lRadius, lPixelSpacing, iPixelSpacingBits);
  PrintInfo(iPixelSpacingBits) ;
  // zoom = decrease radius 
  lRadius /=2.0;
  

  }

  


 return 0;
}


And result is : 

Magnification = 6.666667e-01 ; radius = 1.500000e+00 ; PixelSpacing = 3.000000e-03 ; PixelSpacingBits = 8 use float 
Magnification = 1.333333e+00 ; radius = 7.500000e-01 ; PixelSpacing = 1.500000e-03 ; PixelSpacingBits = 9 use float 
Magnification = 2.666667e+00 ; radius = 3.750000e-01 ; PixelSpacing = 7.500000e-04 ; PixelSpacingBits = 10 use float 
Magnification = 5.333333e+00 ; radius = 1.875000e-01 ; PixelSpacing = 3.750000e-04 ; PixelSpacingBits = 11 use float 
Magnification = 1.066667e+01 ; radius = 9.375000e-02 ; PixelSpacing = 1.875000e-04 ; PixelSpacingBits = 12 use float 
...
Magnification = 7.158279e+08 ; radius = 1.396984e-09 ; PixelSpacing = 2.793968e-12 ; PixelSpacingBits = 38 use float 
Magnification = 1.431656e+09 ; radius = 6.984919e-10 ; PixelSpacing = 1.396984e-12 ; PixelSpacingBits = 39 use float 
Magnification = 2.863312e+09 ; radius = 3.492460e-10 ; PixelSpacing = 6.984919e-13 ; PixelSpacingBits = 40 use float 
Magnification = 5.726623e+09 ; radius = 1.746230e-10 ; PixelSpacing = 3.492460e-13 ; PixelSpacingBits = 41 use double 
Magnification = 1.145325e+10 ; radius = 8.731149e-11 ; PixelSpacing = 1.746230e-13 ; PixelSpacingBits = 42 use double 
Magnification = 2.290649e+10 ; radius = 4.365575e-11 ; PixelSpacing = 8.731149e-14 ; PixelSpacingBits = 43 use double 
Magnification = 4.581298e+10 ; radius = 2.182787e-11 ; PixelSpacing = 4.365575e-14 ; PixelSpacingBits = 44 use double 
Magnification = 9.162597e+10 ; radius = 1.091394e-11 ; PixelSpacing = 2.182787e-14 ; PixelSpacingBits = 45 use double 
Magnification = 1.832519e+11 ; radius = 5.456968e-12 ; PixelSpacing = 1.091394e-14 ; PixelSpacingBits = 46 use double 
Magnification = 3.665039e+11 ; radius = 2.728484e-12 ; PixelSpacing = 5.456968e-15 ; PixelSpacingBits = 47 use double 
Magnification = 7.330078e+11 ; radius = 1.364242e-12 ; PixelSpacing = 2.728484e-15 ; PixelSpacingBits = 48 use double 
Magnification = 1.466016e+12 ; radius = 6.821210e-13 ; PixelSpacing = 1.364242e-15 ; PixelSpacingBits = 49 use double 
Magnification = 2.932031e+12 ; radius = 3.410605e-13 ; PixelSpacing = 6.821210e-16 ; PixelSpacingBits = 50 use double 
Magnification = 5.864062e+12 ; radius = 1.705303e-13 ; PixelSpacing = 3.410605e-16 ; PixelSpacingBits = 51 use long double 
Magnification = 1.172812e+13 ; radius = 8.526513e-14 ; PixelSpacing = 1.705303e-16 ; PixelSpacingBits = 52 use long double 
Magnification = 2.345625e+13 ; radius = 4.263256e-14 ; PixelSpacing = 8.526513e-17 ; PixelSpacingBits = 53 use long double 
Magnification = 4.691250e+13 ; radius = 2.131628e-14 ; PixelSpacing = 4.263256e-17 ; PixelSpacingBits = 54 use long double 
Magnification = 9.382499e+13 ; radius = 1.065814e-14 ; PixelSpacing = 2.131628e-17 ; PixelSpacingBits = 55 use long double 
Magnification = 1.876500e+14 ; radius = 5.329071e-15 ; PixelSpacing = 1.065814e-17 ; PixelSpacingBits = 56 use long double 
Magnification = 3.753000e+14 ; radius = 2.664535e-15 ; PixelSpacing = 5.329071e-18 ; PixelSpacingBits = 57 use long double 
Magnification = 7.505999e+14 ; radius = 1.332268e-15 ; PixelSpacing = 2.664535e-18 ; PixelSpacingBits = 58 use long double 
Magnification = 1.501200e+15 ; radius = 6.661338e-16 ; PixelSpacing = 1.332268e-18 ; PixelSpacingBits = 59 use long double 
Magnification = 3.002400e+15 ; radius = 3.330669e-16 ; PixelSpacing = 6.661338e-19 ; PixelSpacingBits = 60 use long double 
Magnification = 6.004800e+15 ; radius = 1.665335e-16 ; PixelSpacing = 3.330669e-19 ; PixelSpacingBits = 61 use arbitrary precision number, like MPFR 
Magnification = 1.200960e+16 ; radius = 8.326673e-17 ; PixelSpacing = 1.665335e-19 ; PixelSpacingBits = 62 use arbitrary precision number, like MPFR 
Magnification = 2.401920e+16 ; radius = 4.163336e-17 ; PixelSpacing = 8.326673e-20 ; PixelSpacingBits = 63 use arbitrary precision number, like MPFR 
Magnification = 4.803840e+16 ; radius = 2.081668e-17 ; PixelSpacing = 4.163336e-20 ; PixelSpacingBits = 64 use arbitrary precision number, like MPFR 
Magnification = 9.607679e+16 ; radius = 1.040834e-17 ; PixelSpacing = 2.081668e-20 ; PixelSpacingBits = 65 use arbitrary precision number, like MPFR 
Magnification = 1.921536e+17 ; radius = 5.204170e-18 ; PixelSpacing = 1.040834e-20 ; PixelSpacingBits = 66 use arbitrary precision number, like MPFR 
Magnification = 3.843072e+17 ; radius = 2.602085e-18 ; PixelSpacing = 5.204170e-21 ; PixelSpacingBits = 67 use arbitrary precision number, like MPFR 
Magnification = 7.686143e+17 ; radius = 1.301043e-18 ; PixelSpacing = 2.602085e-21 ; PixelSpacingBits = 68 use arbitrary precision number, like MPFR 
Magnification = 1.537229e+18 ; radius = 6.505213e-19 ; PixelSpacing = 1.301043e-21 ; PixelSpacingBits = 69 use arbitrary precision number, like MPFR 
Magnification = 3.074457e+18 ; radius = 3.252607e-19 ; PixelSpacing = 6.505213e-22 ; PixelSpacingBits = 70 use arbitrary precision number, like MPFR 
Magnification = 6.148915e+18 ; radius = 1.626303e-19 ; PixelSpacing = 3.252607e-22 ; PixelSpacingBits = 71 use arbitrary precision number, like MPFR 
Magnification = 1.229783e+19 ; radius = 8.131516e-20 ; PixelSpacing = 1.626303e-22 ; PixelSpacingBits = 72 use arbitrary precision number, like MPFR 
Magnification = 2.459566e+19 ; radius = 4.065758e-20 ; PixelSpacing = 8.131516e-23 ; PixelSpacingBits = 73 use arbitrary precision number, like MPFR

Examples

Baby Monster by DinkydauSet[47] : zoom into parameter plane of complex quadratic polynomial :


program : mandel machine x one week ( 4000x3000 ) 
algorithm : escape time 
precision = 7000
magnification = 2^(6901.591) = 3.8539742140068607747447368372813E2077 = 3.8539742140068607747447368372813 *10^(2077)
centerRe =      0.4026223242141852148037824724584025835755135011342881027042525627039569502881670946745557412930327115393258794913548834454537746442641230778661250740808696667685167031459830818673342528174897920124209545137508922550549968221550363823064128549715028301461622593069839496780093952808237573205197164572673594064416772605893796305663235635527880132594672201779519565231079208219169990178251347386228988056919160862667394171741551928464324300754658056232719271701044207283382298845257395452425798232763791743779314353854383722879333193167946859425243707261854429090471722384741345982162350257163211439072535377347476863063971161548476045589432821456788895124531684440296396587503362225268140306547818930627963692042601813606866625158984034539104729252270036522838631376204929633117350514392534098621950298874921561848480721715466716034612641357006597673782157926191463771077735121499521415799630479650549024192802530771425233126786755033877940979179549256821540572419329726522803422394291516882903607750877675838298417678464016201757067174161515701977269714418733430534088597594663546370996913330820306039197466323342547246232849027813752870111841998012412400077840383443533115591420661427063968799614034835064533287768378088050419077884398682152379426978057892246066882890819414748458464211672718229513050617638747371353729091501912075437789263019440768014217748069621815249161576890441895414789868155359854876653884160567578413850597585526839599148529091786964892859271522516203113708568784835766360055829328924133199024188688844937378174198793904588311188393798698747503071556711010350663949412136302614381521786902283300674108990630100130448100638953468850976478379826240732566854132975350164428623726436941877225968956042433264823693750422381553726384657388053048021285450658976425595261910844568695172761539871359485880883688256972852102360571149799163601150837375544386512748326612079156006358192675222805435405708616040869538348696626733367203267216061599286266159729225868003852298996109238906739358339973449675179531666048724844664052031271387710787740075700568712301627930122446
centerIm = 0.3414661267010330639258781735300664742792277354243426548082347808924808079842063432641337745084491842274928006043526205335660078979452366866756969329129441667312564036874357179068281915055443525509599130331320610821012236201307641349065669509178006415633193858304674801753225345910395424302568889690765898697389344506716385444532416760848755811454604769082865518885687677043988923482755514450647501464529277548626228211775326421789838725360483456061933115401603120908257520719931828418717929225819541974242262149693721546436344398096633938554552017842417617179797586236724871081452420464280333125369667508863083941830427529275353658367633700463591140837752713130326658698539827580385561537043307893113743040288109423825683661313727523597674848484087312515923976610370831729746783850452751041682640731573001319728478688445020726240850018852640901126812894024112093280413500010748891409049642255971933031658182432137372842717466247939807168712399315317154441773203170047657667231871264210848409477591021867775954396341273647285869183323193925375356957738345603739082474205799801007250041854109282041356811030974599202640896266028843535401330225609771341865327032085135831902603640939226040984911910075236054433300263457714999659548633581618107640012502951867204419221851370812448359108387310012121047998792211175821507898822472067545566323088233165752919891462234618228444539224969139541397976528218516885487556195557179718372941445119064646137527396209369577296787387634243210140885928439211898265659865402840837723799792668419799443445421585714176943014398043568698898179253868782669987422851258992794036747294932260334459254264688360704250224826019403156200812024463700689508527620855762445523530566725311570637375162222843632726633580544365800704348649164263654725083759306974477081672768736376743801103735815276810809861222374937053298147754358060737309317498277835724639189151138998429279826787118135717747963875281826078928680133524179137446312206008103340479076493412664529374765456320670666843471865606806283972354009907403302001818229385746724505497627613149001435837120422584
iterationMax = 35 000 000


Cross Hair by Claude Heiland-Allen .[48] Below is the content of kfr file ( parameter for Kalles Fraktaler )[49]

Re: -1.94156695046089411519723545042405785041614289882129276726563682132425517088701591901639765783026799492137462058533435865811646793455507945
Im: -0.00017301617109765913618843129805085094212526763902256359889382674446838992551267030035919209576862092841923454016429306276671035659004195
Zoom: 3.15216049570E116
Iterations: 203416
IterDiv: 1.000000
SmoothMethod: 0
ColorMethod: 0
ColorOffset: 0
Rotate: 0.000000
Ratio: 360
Colors: 0,0,0,41,35,190,132,225,108,214,174,82,144,73,241,241,187,233,235,179,166,219,60,135,12,62,153,36,94,13,28,6,183,71,222,179,18,77,200,67,187,139,166,31,3,90,125,9,56,37,31,93,212,203,252,150,245,69,59,19,13,137,10,28,219,174,50,32,154,80,238,64,120,54,253,18,73,50,246,158,125,73,220,173,79,20,242,68,64,102,208,107,196,48,183,50,59,161,34,246,34,145,157,225,139,31,218,176,202,153,2,185,114,157,73,44,128,126,197,153,213,233,128,178,234,201,204,83,191,103,214,191,20,214,126,45,220,142,102,131,239,87,73,97,255,105,143,97,205,209,30,157,156,22,114,114,230,29,240,132,79,74,119,2,215,232,57,44,83,203,201,18,30,51,116,158,12,244,213,212,159,212,164,89,126,53,207,50,34,244,204,207,211,144,45,72,211,143,117,230,217,29,42,229,192,247,43,120,129,135,68,14,95,80,0,212,97,141,190,123,5,21,7,59,51,130,31,24,112,146,218,100,84,206,177,133,62,105,21,248,70,106,4,150,115,14,217,22,47,103,104,212,247,74,74,208,87,104,118,250,22,187,17,173,174,36,136,121,254,82,219,37,67,229,60,244,69,211,216,40,206,11,245,197,96,89,61,151,39,138,89,118,45,208,194,201,205,104,212,73,106,121,37,8,97,64,20,177,59,106,165,17,40,193,140,214,169,11,135,151,140,47,241,21,29,154,149,193,155,225,192,126,233,168,154,167,134,194,181,84,191,154,231,217,35,209,85,144,56,40,209,217,108,161,102,94,78,225,48,156,254,217,113,159,226,165,226,12,155,180,71,101,56,42,70,137,169,130,121,122,118,120,194,99,
Smooth: 1
MultiColor: 0
BlendMC: 0
MultiColors: 
Power: 2
FractalType: 0



# example by Dinkydau : http://www.fractalforums.com/announcements-and-news/superfractalthing-arbitrary-precision-mandelbrot-set-rendering-in-java/
Re = -1.479,946,223,325,078,880,202,580,653,442,563,833,590,828,874,828,533,272,328,919,467,504,501,428,041,551,458,102,123,157,715,213,651,035,545,943,542,078,167,348,953,885,787,341,902,612,509,986,72
Im = 0.000,901,397,329,020,353,980,197,791,866,197,173,566,251,566,818,045,102,411,067,630,386,488,692,287,189,049,145,621,584,436,026,934,218,763,527,577,290,631,809,454,796,618,110,767,424,580,322,79
Magnification = 2^471 = 6.0971651373359223269171820894398 E141

List :

Möbius transformation

Riemann sphere

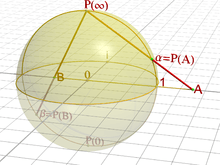
A Möbius transformation[50] of the extended complex plane ( the Riemann sphere ) :


is a rational function with general for :

It's inverse function in general form is :

Specifying a transformation by three points

Given a set of three distinct points z1, z2, z3 on the one Riemann sphere ( let's call it z-sphere) and a second set of distinct points w1, w2, w3 on the second sphere ( w-sphere) , there exists precisely one Möbius transformation f(z) with :

for i=1,2,3

Mapping to 0, 1, infinity

The Möbius transformation with an explicit formula :[51]

maps :

the unit circle to the real axis - first method

Let's choose 3 z points on a circle :

then the Möbius transformation will be :

Knowing that : [52]

one can simplify this to :

In Maxima CAS one can do it :

(%i1) rectform((z+1)*(%i-1)/((z-1)*(%i+1)));
(%o1) (%i*(z+1))/(z−1)

where coefficients of the general form are :

so inverse function can be computed using general form :

Lets check it using Maxima CAS : 

(%i3) fi(w):=(-%i-w)/(%i-w);
(%o3) fi(w):=−%i−w/%i−w
(%i4) fi(0);
(%o4) −1
(%i5) fi(1);
(%o5) −%i−1/%i−1
(%i6) rectform(%);
(%o6) %i

Find how to compute it without symbolic computation program (CAS)  : 

(%i3) fi(w):=(-%i-w)/(%i-w);
(%o3) fi(w):=−%i−w/%i−w
(%i8) z:x+y*%i;
(%o8) %i*y+x
(%i9) z1:fi(w);
(%o9) (−%i*y−x−%i)/(−%i*y−x+%i)
(%i10) realpart(z1);
(%o10) ((−y−1)*(1−y))/((1−y)^2+x^2)+x^2/((1−y)^2+x^2)
(%i11) imagpart(z1);
(%o11) (x*(1−y))/((1−y)^2+x^2)−(x*(−y−1))/((1−y)^2+x^2)
(%i13) ratsimp(realpart(z1));
(%o13) (y^2+x^2−1)/(y^2−2*y+x^2+1)
(%i14) ratsimp(imagpart(z1));
(%o14) (2*x)/(y^2−2*y+x^2+1)
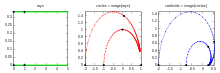
2 steps of unrolling the main cardioid of Mandelbrot set: Moebius map and conformal map
Unrolled main cardioid of Mandelbrot set for periods 7-13

So using notation :

one gets :


It can be used for unrolling the Mandelbrot set components [53]

the unit circle to the real axis - second method

Function :

sends the unit circle to the real axis :

Mapping to the imaginary axis

Function sends the unit circle to the imaginary axis.[54]

References

  1. ↑ wikipedia : Coordinate_system
  2. ↑ viewport in wikipedia
  3. ↑ How to convert world to screen coordinates and vice versa
  4. ↑ | How to transform 2D world to screen coordinates OpenGL
  5. ↑ Mightymandel doc
  6. ↑ Xaos - view
  7. ↑ Claude Heiland-Allen blog
  8. ↑ michael hogg : fractalnet
  9. ↑ optimizing zoom animations by Claude Heiland-Allen
  10. ↑ Fractint Drawing Methods
  11. ↑ Synchronous-Orbit Algorithm by R Munafo
  12. ↑ The Almond BreadHomepage by Michael R. Ganss
  13. ↑ Rough Mandelbrot Sets by Neural Outlet.. posted on 23/11/2014
  14. ↑ Images of Julia sets that you can trust by Luiz Henrique de Figueiredo, Diego Nehab, Jorge Stolfi, and Joao Batista Oliveira
  15. ↑ Weisstein, Eric W. "Parabolic Cylindrical Coordinates." From MathWorld--A Wolfram Web Resource
  16. ↑ Weisstein, Eric W. "Parabolic Coordinates." From MathWorld--A Wolfram Web Resource.
  17. ↑ [http/Fwww.diva-portal.org/smash/Fdiva2/FFULLTEXT01.pdf Numerical approximation of conformal mappings by Bjørnar Steinnes Luteberget]
  18. ↑ processing : transform2d
  19. ↑ Spherical Projections (Stereographic and Cylindrical) Written by Paul Bourke
  20. ↑ Weisstein, Eric W. "Cylindrical Projection." From MathWorld--A Wolfram Web Resource.
  21. ↑ johndcook : joukowsky-transformation
  22. ↑ Exponential mapping with Kalles Fraktaler by Claude Heiland-Allen
  23. ↑ kf-extras for manipulating output from Kalles Fraktaler 2
  24. ↑ Mandelbrot set images and videos by David Madore
  25. ↑ [http://arxiv.org/abs/astro-ph/?0310571 A Map of the Universe by J. Richard Gott III, Mario Jurić, David Schlegel, Fiona Hoyle, Michael Vogeley, Max Tegmark, Neta Bahcall, Jon Brinkmann]
  26. ↑ xkcd : Depth
  27. ↑ Mercator Mandelbrot by Anders Sandberg
  28. ↑ Exponential map by R Munafo
  29. ↑ stackoverflow : how-do-i-zoom-into-the-mandelbrot-set
  30. ↑ Fractal Forum > Fractal Art > Images Showcase (Rate My Fractal) > Baby Monster
  31. ↑ zoom level definition
  32. ↑ Fractal Journey by ORSON WANG
  33. ↑ Zoom level discussion - Maximum zoom level supported by Fractal eXtreme
  34. ↑ fractalforums : history-of-deep-zoom-records
  35. ↑ fractint deep_zoom
  36. ↑ zooming with exteded precision in Delphi
  37. ↑ video Mandelbrot Zoom 999 on youtube by phaumann
  38. ↑ DeepZooming with FractInt
  39. ↑ Mandelbrot set detail Glimpse of variety by DinkydauSet
  40. ↑ e10000 by by Claude Heiland-Allen
  41. ↑ [:w:wiki/Talk:Floating_point/Archive_4#No_mention_of_Double-double No_mention_of_Double-double - talk]
  42. ↑ stackoverflow : mandelbrot-set-reaches-to-its-limit-way-too-soon
  43. ↑ fractalforums : problem with zooming transform one view rect-to another
  44. ↑ fractalforums "basic-location-and-zoom-question
  45. ↑ optimizing_zoom_animations by Claude Heiland-Allen
  46. ↑ fractalforums about-precision-of-doubles
  47. ↑ Baby Monster by DinkydauSet
  48. ↑ Cross Hair by Claude Heiland-Allen
  49. ↑ Kalles Fraktaler 2 by Karl Runmo
  50. ↑ Moebius transformation animated GIFs by Fritz Mueller
  51. ↑ Triple transitivity by David J Wright 2004-12-04
  52. ↑ math.stackexchange questions : how-to-do-this-transformation-of-complex-rational-function
  53. ↑ Stretching cusps by Claude Heiland-Allen
  54. ↑ math.stackexchange questions: what-mobius-transformation-maps-the-unit-circle-z-z-1-to-the-real-axis/335061#335061
This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.