Formal Logic/Sentential Logic/Substitution and Interchange
< Formal Logic < Sentential Logic| ← Properties of Sentential Connectives | ↑ Sentential Logic | Translations → |
Substitution and Interchange
This page will use the notions of occurrence and subformula introduced at the Additional terminology section of Formal Syntax. These notions have been little used if at all since then, so you might want to review them.
Substitution
Tautological forms
We have introduced a number of tautologies, one example being
- (1)
This has the (informally written) form
- (2)
As it turns out, any formula matching this form is a tautology. Thus, for example,
- (3)
is a tautology. This process is general. Take any tautology. Find its most fully explicitly form by uniformly replacing distinct sentence letters with distinct Greek letters. We can call this a tautological form, which will not be a formula but rather a metalogical expression. Any instance of this tautological form is a tautology.
Substitution instances
The preceding illustrated how we can generate new tautologies from old ones via tautological forms. Here, we will show how to generate tautologies without resort to tautological forms. To do this, we will define a substitution instance of a formula. Any substitution instance of a tautology is also a tautology.
First, we define the simple substitution instance of a formula for a sentence letter. Let and be formulae and be a sentence letter. The simple substitution instance is the result of replacing every occurrence of in with an occurrence of . A substitution instance of formulae for a sentence letters is the result of a chain of simple substitution instances. In particular, a chain of zero simple substitutions instances starting from is a substitution instance and indeed is just itself. Thus, any formula is a substitution instance of itself.
![{\displaystyle \varphi [\pi /\psi ]\,\!}](../I/m/d2eebfcef8dc9c38d2c05d12e2f5f0a0e35616de.svg)
It turns out that if is a tautology, then so is any simple substitution instance . If we start with a tautology and generate a chain of simple substitution instances, then every formula in the chain is also a tautology. Thus any (not necessarily simple) substitution instance of a tautology is also a tautology.
Substitution examples
Consider (1) again. We substitute for every occurrence of in (1). This gives us the following simple substitution instance of (1):
- (4)
In this, we substitute for . That gives us (3) as a simple substitution instance of (4). Since (3) is the result of a chain of two simple substitution instances, it is a (non-simple) substitution instance of (1) Since (1) is a tautology, so is (3). We can express the chain of substitutions as
![{\displaystyle \mathrm {Q} \rightarrow (\mathrm {P} \rightarrow \mathrm {Q} )[\mathrm {Q} /\mathrm {R} \land \mathrm {S} ][\mathrm {P} /\mathrm {P} \lor \mathrm {Q} ]\,\!}](../I/m/81271051059723595e8d452d27da89f1af994693.svg)
Take another example, also starting from (1). We want to obtain
- (5)
Our first attempt won't work. First we substitute for obtaining
Next we substitute for obtaining
- (6)
This is indeed a tautology, but it is not the one we wanted. Let's try again. In (1), we substitute for obtaining
Now substitute for obtaining
Finally, substituting for gets us the result we wanted, namely (5). Since (1) is a tautology, so is (5). We can express the chain of substitutions as
![{\displaystyle \mathrm {Q} \rightarrow (\mathrm {P} \rightarrow \mathrm {Q} )[\mathrm {P} /\mathrm {R} ][\mathrm {Q} /\mathrm {P} ][\mathrm {R} /\mathrm {Q} ]\!}](../I/m/3a6dac03fc4768317ce9e57ee664b4a38cd4dfcf.svg)
Simultaneous substitutions
We can compress a chain of simple substitutions into a single complex substitution. Let , , , ... be formulae; let , , ... be sentence letters. We define a simultaneous substitution instance of formulas for sentence letters be the result of starting with and simultaneously replacing with , with , .... We can regenerate our examples.
![{\displaystyle \varphi [\pi _{1}/\psi _{1},\ \pi _{2}/\psi _{2},\ ...]\,\!}](../I/m/97abe1a722c3e0bec01154fbe24631634c4e7ecf.svg)
The previously generated formula (3) is
![{\displaystyle \mathrm {Q} \rightarrow (\mathrm {P} \rightarrow \mathrm {Q} )[\mathrm {P} /\mathrm {P} \lor \mathrm {Q} ,\mathrm {Q} /\mathrm {R} \land \mathrm {S} ]\,\!}](../I/m/86e6d375945f1499a1f619e0362ac3cb4bec2b09.svg)
Similarly, (5) is
![{\displaystyle \mathrm {Q} \rightarrow (\mathrm {P} \rightarrow \mathrm {Q} )[\mathrm {P} /\mathrm {Q} ,\ \mathrm {Q} /\mathrm {P} ]\,\!}](../I/m/e422947c6c27eebd07aa0cf66ed74321e18f1561.svg)
Finally (6) is
![{\displaystyle \mathrm {Q} \rightarrow (\mathrm {P} \rightarrow \mathrm {Q} )[\mathrm {Q} /\mathrm {P} ]\,\!}](../I/m/dfca8b9e7c07ffb3fd96e9180eda01663234be6f.svg)
When we get to predicate logic, simultaneous substitution instances will not be available. That is why we defined substitution instance by reference to a chain of simple substitution instances rather than as a simultaneous substitution instance.
Interchange
Interchange of equivalent subformulae
We previously saw the following equivalence at Properties of Sentential Connectives:
- (7)
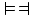
You then might expect the following equivalence:
This expectation is correct; the two formulae are equivalent. Let and be equivalent formulae. Let be a formula in which occurs as a subformula. Finally, let be the result of replacing in at least one (not necessarily all) occurrences of with . Then and are equivalent. This replacement is called an interchange.
For a second example, suppose we want to generate the equivalence
- (8)
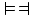
We note the following equivalence:
- (9)
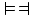
These two formulae can be confirmed to be equivalent either by truth table or, more easily, by substituting for in both formulae of (7).
This substitution does indeed establish (9) as an equivalence. We already noted that and are equivalent if and only if is a tautology. Based on (7), we get the tautology
Our substitution then yields
which is also a tautology. The corresponding equivalence is then (9).
Based on (9), we can now replace the consequent of with its equivalent. This generates the desired equivalence, namely (8).
Every formula equivalent to a tautology is also a tautology. Thus an interchange of equivalent subformulae within a tautology results in a tautology. For example, we can use the substitution instance of (7):
together with the tautology previously seen at Properties of Sentential Connectives:
to obtain
as a new tautology.
Interchange example
As an example, we will use the interdefinability of connectives to express
- (10)
using only conditionals and negations.
Based on
we get the substitution instance
which in turn allows us to replace the appropriate subformula in (10) to get:
- (11)
The equivalence
together with the appropriate substitution gives us
- (12)
as equivalent to (11).
Finally, applying
together with the appropriate substitution, yields our final result:
Summary
This page has presented two claims.
- A substitution instance of a tautology is also a tautology.
- Given a formula, the result of interchanging a subformula with an equivalent is a formula equivalent to the given formula.
These claims are not trivial observations or the result of a simple truth table. They are substantial claims that need proof. Proofs are available in a number of standard metalogic textbooks, but are not presented here.