Engineering Tables/Laplace Transform Table 2

< Engineering Tables
ID Function Time domain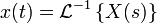
x(t) = \mathcal{L}^{-1} \left\{ X(s) \right\}		 Laplace domain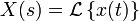
X(s) = \mathcal{L}\left\{ x(t) \right\}		 Region of convergence
for causal systems
1 Ideal delay 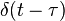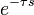\delta(t-\tau) \ e^{-\tau s} \
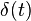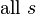1a Unit impulse \delta(t) \ 1 \ \mathrm{all} \ s \,
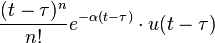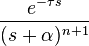2 Delayed nth power with frequency shift \frac{(t-\tau)^n}{n!} e^{-\alpha (t-\tau)} \cdot u(t-\tau) \frac{e^{-\tau s}}{(s+\alpha)^{n+1}} s > 0 \,
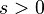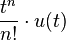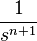2a nth Power { t^n \over n! } \cdot u(t) { 1 \over s^{n+1} } s > 0 \,
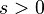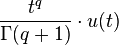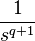2a.1 qth Power { t^q \over \Gamma(q+1) } \cdot u(t) { 1 \over s^{q+1} } s > 0 \,
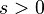2a.2 Unit step 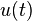u(t) \ { 1 \over s } s > 0 \,
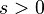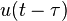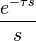2b Delayed unit step u(t-\tau) \ { e^{-\tau s} \over s } s > 0 \,
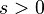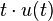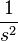2c Ramp t \cdot u(t)\ \frac{1}{s^2} s > 0 \,
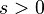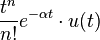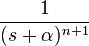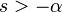2d nth Power with frequency shift \frac{t^{n}}{n!}e^{-\alpha t} \cdot u(t) \frac{1}{(s+\alpha)^{n+1}} s > - \alpha \,
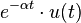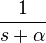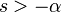2d.1 Exponential decay e^{-\alpha t} \cdot u(t) \ { 1 \over s+\alpha } s > - \alpha \
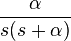3 Exponential approach ( 1-e^{-\alpha t}) \cdot u(t) \ \frac{\alpha}{s(s+\alpha)} s > 0\
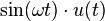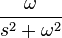4 Sine \sin(\omega t) \cdot u(t) \ { \omega \over s^2 + \omega^2 } s > 0 \
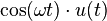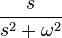5 Cosine \cos(\omega t) \cdot u(t) \ { s \over s^2 + \omega^2 } s > 0 \
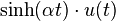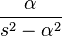6 Hyperbolic sine \sinh(\alpha t) \cdot u(t) \ { \alpha \over s^2 - \alpha^2 } s > | \alpha | \
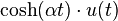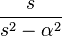7 Hyperbolic cosine \cosh(\alpha t) \cdot u(t) \ { s \over s^2 - \alpha^2 } s > | \alpha | \
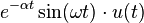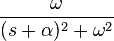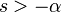8 Exponentially-decaying sine e^{-\alpha t} \sin(\omega t) \cdot u(t) \ { \omega \over (s+\alpha )^2 + \omega^2 } s > -\alpha \
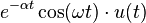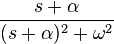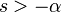9 Exponentially-decaying cosine e^{-\alpha t} \cos(\omega t) \cdot u(t) \ { s+\alpha \over (s+\alpha )^2 + \omega^2 } s > -\alpha \
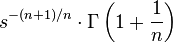10 nth Root \sqrt[n]{t} \cdot u(t) s^{-(n+1)/n} \cdot \Gamma\left(1+\frac{1}{n}\right) s > 0 \,
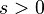11 Natural logarithm 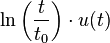\ln \left ( { t \over t_0 } \right ) \cdot u(t) - { t_0 \over s} \ [ \ \ln(t_0 s)+\gamma \ ] s > 0 \,
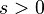12 Bessel function
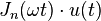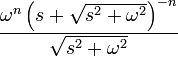of the first kind, of order n		 J_n( \omega t) \cdot u(t) \frac{ \omega^n \left(s+\sqrt{s^2+ \omega^2}\right)^{-n}}{\sqrt{s^2 + \omega^2}} s > 0 \,
(n > -1) \,
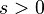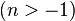13 Modified Bessel function
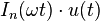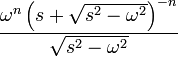of the first kind, of order n		 I_n(\omega t) \cdot u(t) \frac{ \omega^n \left(s+\sqrt{s^2-\omega^2}\right)^{-n}}{\sqrt{s^2-\omega^2}} s > | \omega | \,
14 Bessel function
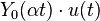of the second kind, of order 0		 Y_0(\alpha t) \cdot u(t)    
15 Modified Bessel function
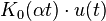of the second kind, of order 0		 K_0(\alpha t) \cdot u(t)    
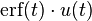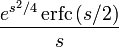16 Error function \mathrm{erf}(t) \cdot u(t) {e^{s^2/4} \operatorname{erfc} \left(s/2\right) \over s} s > 0 \,
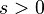Explanatory notes:

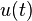  • u(t) \, represents the Heaviside step function.
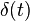  • \delta(t) \, represents the Dirac delta function.
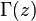  • \Gamma (z) \, represents the Gamma function.
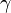  • \gamma \, is the Euler-Mascheroni constant.
  • t \, , a real number, typically represents time,
    although it can represent any independent dimension.
  • s \, is the complex angular frequency.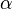
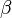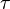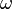  • \alpha \,, \beta \,, \tau \, , and \omega \, are real numbers.
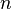  • n \, is an integer.
  • A causal system is a system where the impulse response h(t) is zero for all time t prior to t = 0. In general, the ROC for causal systems is not the same as the ROC for anticausal systems. See also causality.
This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.