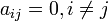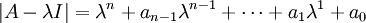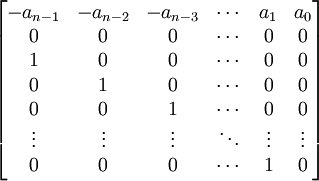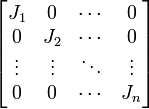Engineering Analysis/Matrix Forms

< Engineering Analysis

Matrices that follow certain predefined formats are useful in a number of computations. We will discuss some of the common matrix formats here. Later chapters will show how these formats are used in calculations and analysis.

Diagonal Matrix

A diagonal matrix is a matrix such that:

a_{ij} = 0, i \ne j

In otherwords, all the elements off the main diagonal are zero, and the diagonal elements may be (but don't need to be) non-zero.

Companion Form Matrix

If we have the following characteristic polynomial for a matrix:

|A - \lambda I| = \lambda^n + a_{n-1}\lambda^{n-1} + \cdots + a_1\lambda^1 + a_0

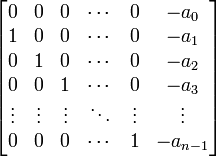
We can create a companion form matrix in one of two ways:

\begin{bmatrix} 0 & 0 & 0 & \cdots & 0 & -a_0 \\ 1 & 0 & 0 & \cdots & 0 & -a_1 \\ 0 & 1 & 0 & \cdots & 0 & -a_2 \\ 0 & 0 & 1 & \cdots & 0 & -a_3 \\ \vdots & \vdots & \vdots &\ddots & \vdots & \vdots \\ 0 & 0 & 0 & \cdots & 1 & -a_{n-1} \end{bmatrix}

Or, we can also write it as:

\begin{bmatrix} -a_{n-1} & -a_{n-2} & -a_{n-3} & \cdots & a_1 & a_0 \\ 0 & 0 & 0 & \cdots & 0 & 0 \\ 1 & 0 & 0 & \cdots & 0 & 0 \\ 0 & 1 & 0 & \cdots & 0 & 0 \\ 0 & 0 & 1 & \cdots & 0 & 0 \\ \vdots & \vdots & \vdots &\ddots & \vdots & \vdots \\ 0 & 0 & 0 & \cdots & 1 & 0 \end{bmatrix}

Jordan Canonical Form

To discuss the Jordan canonical form, we first need to introduce the idea of the Jordan Block:

Jordan Blocks

A jordan block is a square matrix such that all the diagonal elements are equal, and all the super-diagonal elements (the elements directly above the diagonal elements) are all 1. To illustrate this, here is an example of an n-dimensional jordan block:

\begin{bmatrix} a & 1 & 0 & \cdots & 0 \\ 0 & a & 1 & \cdots & 0 \\ 0 & 0 & a & \cdots & 0 \\ \vdots & \vdots & \vdots &\ddots & \vdots \\ 0 & 0 & a & \cdots & 1 \\ 0 & 0 & 0 & \cdots & a \end{bmatrix}

Canonical Form

A square matrix is in Jordan Canonical form, if it is a diagonal matrix, or if it has one of the following two block-diagonal forms:

\begin{bmatrix}D & 0 & \cdots & 0 \\ 0 & J_1 & \cdots & 0 \\ \vdots & \vdots &\ddots & \vdots \\ 0 & 0 & \cdots & J_n \end{bmatrix}

Or:

\begin{bmatrix}J_1 & 0 & \cdots & 0 \\ 0 & J_2 & \cdots & 0 \\ \vdots & \vdots &\ddots & \vdots \\ 0 & 0 & \cdots & J_n \end{bmatrix}

The where the D element is a diagonal block matrix, and the J blocks are in Jordan block form.

This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.