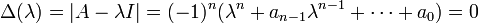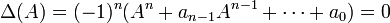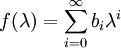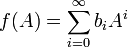Engineering Analysis/Cayley Hamilton Theorem

If the characteristic equation of matrix A is given by:

\Delta(\lambda) = |A-\lambda I| = (-1)^n(\lambda^n + a_{n-1}\lambda^{n-1} + \cdots + a_0) = 0

Then the Cayley-Hamilton theorem states that the matrix A itself is also a valid solution to that equation:

\Delta(A) = (-1)^n(A^n + a_{n-1}A^{n-1} + \cdots + a_0) = 0

Another theorem worth mentioning here (and by "worth mentioning", we really mean "fundamental for some later topics") is stated as:

If λ are the eigenvalues of matrix A, and if there is a function f that is defined as a linear combination of powers of λ:

f(\lambda) = \sum_{i = 0}^\infty b_i \lambda^i

If this function has a radius of convergence S, and if all the eigenvectors of A have magnitudes less then S, then the matrix A itself is also a solution to that function:

f(A) = \sum_{i = 0}^\infty b_i A^i

This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.