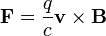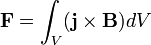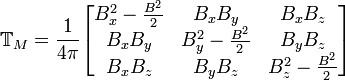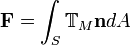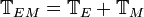Electrodynamics/Magnetic Stress Tensor

< Electrodynamics

Differential Version

\mathbf{F} = \frac{q}{c}\mathbf{v} \times \mathbf{B}

Volume Integral Version

\mathbf{F} = \int_V(\mathbf{j} \times \mathbf{B})dV

Magnetic Stress Tensor

\mathbb{T}_M = \frac{1}{4\pi} \begin{bmatrix} B_x^2 - \frac{B^2}{2} & B_x B_y & B_x B_z \\ B_x B_y & B_y^2 - \frac{B^2}{2} & B_y B_z \\ B_x B_z & B_y B_z & B_z^2 - \frac{B^2}{2} \end{bmatrix}

Surface Integral Version

\mathbf{F} = \int_S \mathbb{T}_M \mathbf{n} dA

Electromagnetic Stress Tensor

If we add our two stress tensors together, piece-wise, we will get a combined electromagnetic stress tensor:

\mathbb{T}_{EM} = \mathbb{T}_E + \mathbb{T}_M

This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.