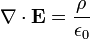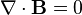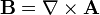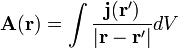Electrodynamics/Magnetic Potential

Gauss' Law of Magnetostatics

Gauss's Law for electrostatics states that

\nabla \cdot \mathbf{E} = \frac{\rho}{\epsilon_0}

This tells us that the source of electric fields are charges. However, experiments show that there are no corresponding "charges"(monopoles) for magnetic field. The magnetic field do not have a source, and so always forms closed loops.

Gauss' law of magnetostatics is an expression of the fact. It can be written as such:

\nabla \cdot \mathbf{B} = 0

Vector Potential

Since B is divergence-free, B must be the curl of some vector A. This vector is called the vector potential, the direct analog of the electric potential, also known as the scalar potential.

The Biot-Savart Law can be difficult to compute directly, but if we know the magnetic potential field, we can find the magnetic field easily:

\mathbf{B} = \nabla \times \mathbf{A}

Calculation of Vector Potential.

The vector potential is given by

\mathbf{A}(\mathbf{r}) = \int \frac{\mathbf{j}(\mathbf{r'})}{|\mathbf{r} - \mathbf{r'}|}dV

This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.