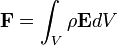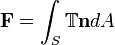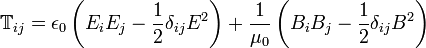Electrodynamics/Electrostatic Stress Tensor

< Electrodynamics

Force on a Charge

When we want to discuss the force on a charge due to a charge distribution, there are two options. The first is a more traditional method: an integral over a volume containing the charge distribution. The second method is less traditional but is easier to do: a surface integral over a special stress tensor.

Volume Integral Version

\mathbf{F} = \int_V \rho \mathbf{E} dV

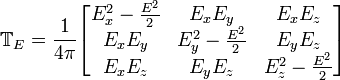
Electrostatic Stress Tensor

\mathbb{T}_E = \frac{1}{4 \pi} \begin{bmatrix} E_x^2 - \frac{E^2}{2} & E_x E_y & E_x E_z \\ E_x E_y & E_y^2 - \frac{E^2}{2} & E_y E_z \\ E_x E_z & E_y E_z & E_z^2 - \frac{E^2}{2} \end{bmatrix}

Surface Integral Version

\mathbf{F} = \int_S \mathbb{T} \mathbf{n} dA

The Maxwell Stress Tensor

Tij is called the Maxwell Stress Tensor, it has two indices and is not a vector so is given a double arrow.

\mathbb{T}_{ij} = \epsilon_0 \left(E_i E_j - \frac{1}{2} \delta_{ij} E^2 \right) + \frac{1}{\mu_0}\left(B_i B_j - \frac{1}{2} \delta_{ij} B^2 \right)
This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.