Econometric Theory/Proofs of properties of β1

Linearity

To be linear, 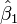$\hat{\beta}_1$ must be a linear function of 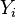$Y_i$ , as shown below

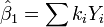
$\hat{\beta}_1 = \sum{k_i Y_i}$

where 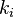$k_i$ is a constant, at any given observation 'i'.

Proof

From the deviation-from-means form of the solution of the OLS Normal Equation for 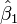$\hat{\beta}_1$ , we have

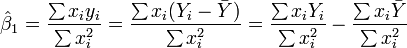
$\hat{\beta}_1 = \frac{\sum{x_i y_i}}{\sum{x^{2}_i}} = \frac{\sum{x_i (Y_i - \bar{Y})}}{\sum{x_{i}^2}} = \frac{\sum{x_i Y_i}}{\sum{x_{i}^2}} - \frac{\sum{x_i \bar{Y}}}{\sum{x_{i}^2}}$

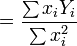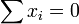$= \frac{\sum{x_i Y_i}}{\sum{x_{i}^2}}$ , since ${\sum{x_i}} = 0$ .

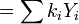$= \sum{k_i Y_i}$ , where 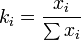$k_i = \frac{x_i}{\sum{x_i}}$ , which is a constant for any given 'i'-value.

This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.