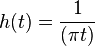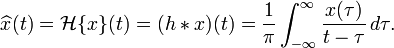Digital Signal Processing/Hilbert Transform

Definition

The Hilbert transform is used to generate a complex signal from a real signal. The Hilbert transform is characterized by the impulse response:

h(t)= {1 \over (\pi t)}

The Hilbert Transform of a function x(t) is the convolution of x(t) with the function h(t), above. The Hilbert Transform is defined as such:

[Hilbert Transform]

\widehat x(t) = \mathcal{H}\{x\}(t) = (h*x)(t) = \frac{1}{\pi}\int_{-\infty}^{\infty}\frac{x(\tau)}{t-\tau}\, d\tau.\,

We use the notation 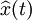$\widehat x(t)$ to denote the hilbert transformation of x(t).

This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.