Conic Sections/Parabola

Definition

The parabola is another commonly known conic section. The geometric definition of a parabola is the locus of all points such that they are equidistant from a point, known as the focus, and a straight line, called the directrix. In other words the eccentricity of a parabola is equal to 1. The solid formed by rotating a parabola about the axis is called a paraboloid.

Graphing Parabola

The general form of a vertical parabola is 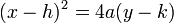$(x - h)^2 = 4a(y-k)$ .

The axis of the parabola is the line perpendicular to the directrix which passes through the focus, and is the line $x = h$ . It is also known as the line of symmetry.
The vertex is the 'base' of the parabola and is located at 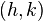$(h, k)$ . Therefore, a positive 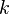$k$ will move the parabola upwards along its axis 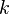$k$ units, while a negative one will move it downwards. This is the same regardless of whether 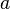$a$ is a positive or negative number.
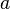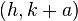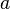$a$ is the focal length of the parabola. The focus is located at $(h, k + a)$ . If $a$ is positive the parabola opens upwards, whereas a negative 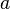$a$ causes it to open downwards.
The directrix is located at $y = k - a$ .

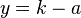If the conic is horizontal, it is the same as a vertical parabola only along the x-axis rather than the y-axis. The general form is: 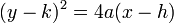$(y - k)^2 = 4a(x-h)$ .

The axis of the parabola is the line $y = k$ .
The vertex is located at 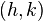$(h, k)$ . A positive 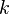$k$ will move the parabola towards the right along its axis 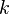$k$ units, while a negative one will move it towards the left. This is the same regardless of whether 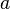$a$ is a positive or negative number.
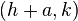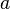The focus is located at $(h + a, k)$ . If $a$ is positive the parabola opens towards the right, whereas a negative 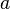$a$ causes it to open leftwards.
The directrix is located at $x = h - a$ .

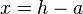Parametric Form

The parametric form of a vertical parabola is:
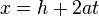
$x=h + 2at$
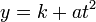
$y=k + at^2$
For a horizontal one:
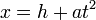
$x=h + at^2$
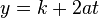
$y=k + 2at$
For both of these forms:

The vertex is at (h,k)
The focus is 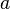$a$ units from the vertex along the major axis.
The gradient at any point on the parabola is t, which can be proved by differentiating the parametric form using the chain rule.

For information on how to graph the paramatric form, see Parametric Forms of Conic Sections.

Polar Form

The polar form of a parabola is given by 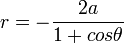$r=-\frac{2a}{1+cos \theta}$ .

Applications

Parabola have a number of uses in everyday life:

Galileo showed in the 16th century that objects fired into the air at an angle to the ground followed the path of a parabola, a discover which led to more accurate of targeting of projectiles.
In optics, parabola are particularly useful because parallel beams incident upon a parabolic mirror are all directed towards the focus, and conversely a light source placed at the focus will reflect off the mirror as a series of parallel rays. This makes parabolic mirrors useful in telescopes, headlights, satellite dishes and much more.
Another use of parabola is in training astronauts. A plane which follows a parabolic path into the air will cause passengers to experience freefall and therefore weightlessness.

References

This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.