Conic Sections/Hyperbola

Definition

A hyperbola can be defined as the locus of all points such that the difference between the distance of each point from two points known as the foci is constant. This is similar to an ellipse, however whereas in an ellipse the distances sum to a constant, here they subtract to one. A hyperbola can also be defined as the locus of all points such that the distance of the point to the closest focus divided by the distance to the directrix, a ratio known as the eccentricity, is a constant greater than one.

Graphing Hyperbolae

The general form of a hyperbola with a horizontal transverse axis, i.e. the axis on which the foci lie, is: 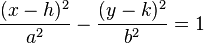$\frac{(x-h)^2}{a^2} - \frac{(y-k)^2}{b^2} = 1$
A hyperbola with a vertical transverse axis, on the other hand, is of the form: 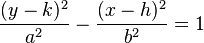$\frac{(y-k)^2}{a^2} - \frac{(x-h)^2}{b^2} = 1$ .

The centre of the hyperbola is $(h,k)$ .
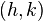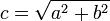The two foci are found at a distance of $c$ from the centre in each direction along the transverse axis, where $c = \sqrt{a^2 + b^2}$ .
The eccentricity of the hyperbola can be found by $\frac{c}{a}$ . A higher eccentricity makes the hyperbola 'steeper', whereas a smaller one makes it more 'curvy'.
The vertices are a distance of 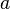$a$ from the centre of the hyperbola in each direction along the transverse axis.
The difference between the distances of any point from each of the foci is equal to $2a$ .
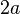Hyperbola also have two asymptotes. An asymptote is a line that points on the graph continuously approach yet never reach. If you extended the graph vast distances along each axis, you would observe it getting closer and closer to the asymptote, however it would never actually reach it. The asymptotes can be found by 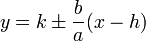$y=k\pm\frac{b}{a}(x-h)$ for a horizontal hyperbola, or 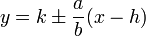$y=k\pm\frac{a}{b}(x-h)$ for a vertical one.

References

This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.